ホームへ 少年少女数学愛好会へ 取れたての定理集へ
ベトナムのハノイにある寺院には、100枚の石板と3本の柱があって、僧侶たちが石版を1枚ずつ移動しているのだそうです。石板は大きい順に下から積み上げられていて、移動する途中で大きい石板が小さい石板の上になってはいけません。僧侶たちは毎日この石板を動かしつづけているのだそうです。そして、この100枚の石板が移動したときに、この世が終わるという言い伝えがあるのだそうです。 この話を、しばらく信じていましたが、これは作り話なんだそうです。・・・ハノイの塔

3本柱のハノイの塔
1枚のときには、1回で移動できることは、明らかです。
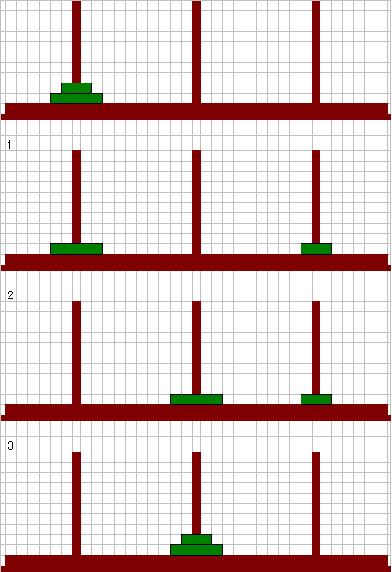
2枚のときには、左図のようにして3回で移動できます。これが最小回数であることも、おそらく文句の無いところだと思います。

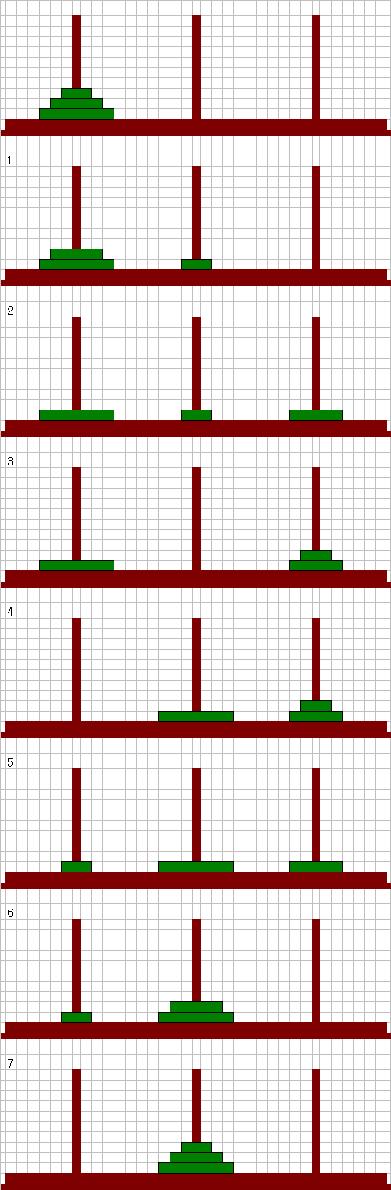
3枚のときには、回数が多くなりますが、左のようにして7回で移動できます。
このハノイの塔に向かって黙々と動かしつづけていると、やり方がつかめてきます。どう動かせばよいか分かってきますが、これを最後までやるのはかなり大変です。何しろ、このハノイの塔は10枚ですから、後で述べるように、1023回かかるのです。こ二日間で、二人の生徒がやり遂げましたが、途中で8止める生徒が多かったようです。

これは4枚の場合です。
全部移動するためには、一番底にある一番大きな円盤を移動しなければなりません。動かすための場所を作るためには、その上にある3枚の円盤を、1本の柱に移動していなければなりません。
左の図は、まず、上から3枚を真中の柱に移動しています。次に、一番大きな円盤を残りの柱に移動し、その後また3枚を移動した大きな円盤の上に重ねています。
これは、一般にn枚のときにもいえることです。n枚の円盤を移動する最小回数をanとしましょう。上から(n−1)枚をan-1回で別の柱に移動させて、一番下の最大の円盤を空いている柱に移動させた後、また、an-1回で残る(n−1)枚を移動させればいいのですから、
an=2an-1+1
という漸化式がなりたちます。
a1=1、an=2an-1+1 から、
an=2n−1
ということになります。
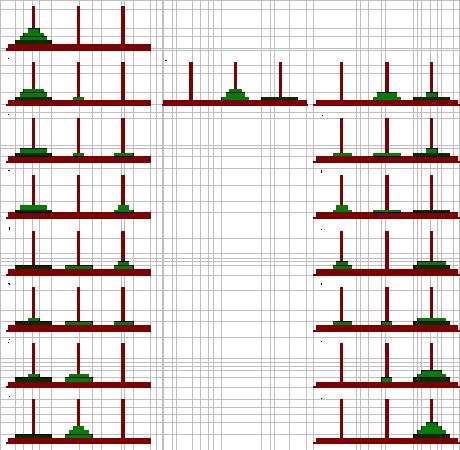
4本ハノイ
柱が2本しかないとすると、このゲームはできません。これができるのは、最低でも柱が3本必要です。この柱が4本になるとどうなるでしょう?
柱が4本になると、自由度が高まる分、移動回数は少なくてすみます。左の図は3枚のときの4本ハノイの移動を示しています。一つの柱に一枚ずつ置いても、まだ1本柱があります。3本ハノイの時には7回かかった移動が4本ハノイでは5回で終わってしまいます。

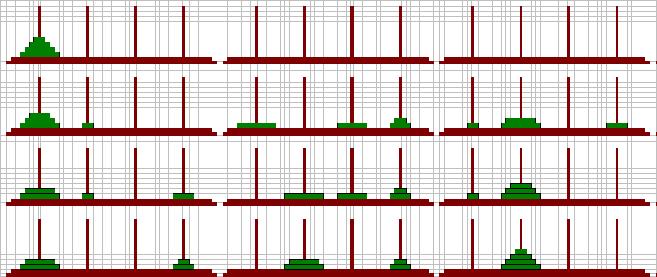
4枚の4本ハノイです。
まず、3回で上の2枚を移動しています。次に、残り2枚を移動してから、その上に小さい2枚を移動しています。
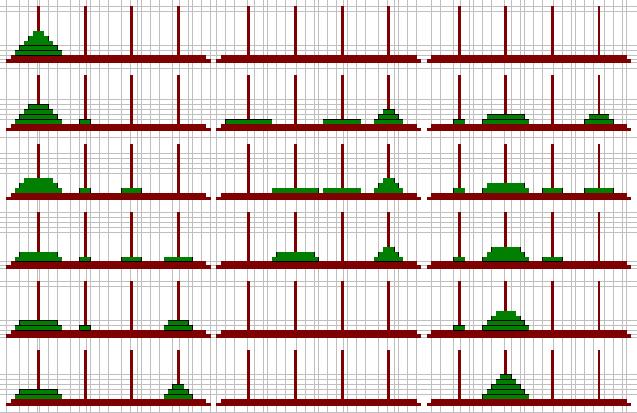
5枚の4本ハノイです。
同じく、下の2枚を残して上3枚を移動しています。上3枚の移動に要する回数は、3枚の4本ハノイの回数だる5回です。次に、下の大きな2枚を移動するときには、上の3枚が置いてある柱以外の3本を使っての移動ですから、2枚の3本ハノイの回数である3回で移動しています。その後、小さい3枚の移動は、また3枚4本ハノイの回数である5回で移動し、合計13回ということになります。
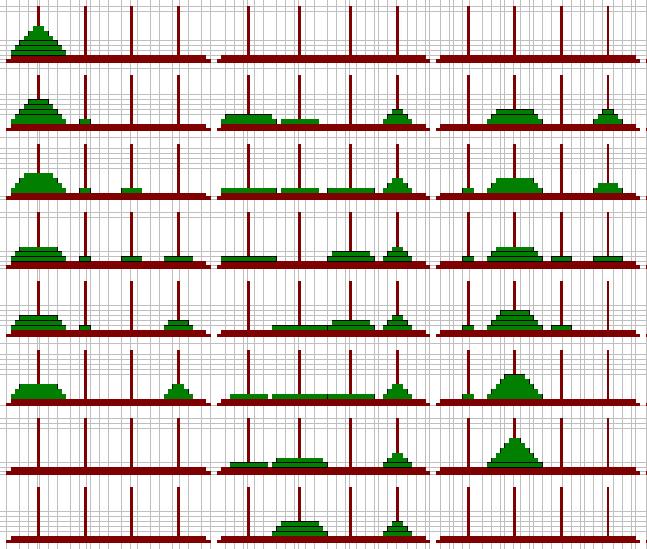
6枚の4本ハノイです。
左の図の移動では、まず上の3枚を5回で移動してから、下の3枚を移動しています。上の3枚が置いてある柱は使えませんから、ここからは3本ハノイの移動の仕方になってしまいます。3枚の3本ハノイで最低でも7回必要となります。そして、その後3枚を移動しますが、これには4本ハノイの5回が必要です。6枚の場合は、このようにして見てみると、17回かかりそうです。
上で見たように、大きいほうの何枚かを残して上の小さい円盤を一つの柱に重ねるまでは、4本ハノイの移動となり、その後、残した大きな円盤の移動は3本ハノイになります。そこで、一枚残した場合、二枚残した場合、三枚残した場合・・・と調べていって下の表のようにまとめてみました。枚数が大きくなるにつれて、残した枚数が多くなったほうが全体の回数が少なくなります。しかし、残した枚数が大きすぎるとまた回数が増えてしまいます。円盤の枚数により、残す円盤の枚数に最適値があることがわかります。このように、何枚残すかで回数を調べていき、それらの中で最小のものを取っていけば、それが4本ハノイの移動の最小回数が分かります。
| 枚数(n) | 4本ハノイ | 3本ハノイ | 一枚残 | 二枚残 | 三枚残 | 四枚残 | 五枚残 | 六枚残 | 七枚残 | 八枚残 | 九枚残 | 十枚残 |
| 1 | 1 | 1 | ||||||||||
| 2 | 3 | 3 | 3 | |||||||||
| 3 | 5 | 7 | 7 | 5 | ||||||||
| 4 | 9 | 15 | 11 | 9 | 9 | |||||||
| 5 | 13 | 31 | 19 | 13 | 13 | 17 | ||||||
| 6 | 17 | 63 | 27 | 21 | 17 | 21 | 33 | |||||
| 7 | 25 | 127 | 35 | 29 | 25 | 25 | 37 | 65 | ||||
| 8 | 33 | 255 | 51 | 37 | 33 | 33 | 41 | 69 | 129 | |||
| 9 | 41 | 511 | 67 | 53 | 41 | 41 | 49 | 73 | 133 | 257 | ||
| 10 | 49 | 1023 | 83 | 69 | 57 | 49 | 57 | 81 | 137 | 261 | 513 | |
| 11 | 65 | 2047 | 99 | 85 | 73 | 65 | 65 | 89 | 145 | 265 | 517 | 1025 |
| 12 | 81 | 4095 | 131 | 101 | 89 | 81 | 81 | 97 | 153 | 273 | 521 | 1029 |
| 13 | 97 | 8191 | 163 | 133 | 105 | 97 | 97 | 113 | 161 | 281 | 529 | 1033 |
| 14 | 113 | 16383 | 195 | 165 | 137 | 113 | 113 | 129 | 177 | 289 | 537 | 1041 |
| 15 | 129 | 32767 | 227 | 197 | 169 | 145 | 129 | 145 | 193 | 305 | 545 | 1049 |
| 16 | 161 | 65535 | 259 | 229 | 201 | 177 | 161 | 161 | 209 | 321 | 561 | 1057 |
4本ハノイの最小手数・・・その規則性
n枚の4本ハノイの移動回数を bn とします。上の表から数列 bn の階差数列を調べてみたら、
2,2,4,4,4,8,8,8,8,16,16,16,16,16,32,32,・・・
この階差数列の数字が変わるところが、何枚残すかによって回数の最小値が移動したところだということまで分かりました。
5本ハノイ
上で考えた方法で5本ハノイも考えることができる。そこで「5本ハノイ」についても考えてみよう。5本棒のハノイの塔は4本棒のハノイの塔に大きく関連していることがわかった。このことは、3本棒のハノイの塔と4本棒のハノイの塔との関係とほぼ、いや、全く同じと言えるでしょう。
ハノイの塔は棒の数と大きな関係があります。諸知識でも述べましたが、ブロックの移動にはどうしても自由に移動が出来るような棒が必要となるのです。しかし、この関係のみでは、4,5本棒のハノイの塔は成り立ちません。と言うか、最小の回数でハノイの塔を完成させることは出来ません。では、そのほかにどんな規則性があるのでしょうか?
我々は、はじめに「5本棒のハノイの塔は4本棒のハノイの塔に大きく関連している」と述べましたが、これは、つまり、5本棒のハノイの塔の中に4本棒のハノイの塔が存在すると言うことである。この性質が現れるのはブロック数個をある他の棒に移したときに現れます。
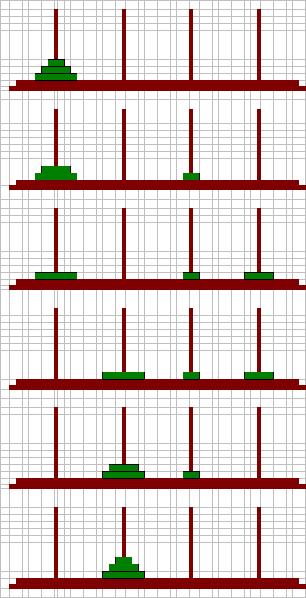
例えば、ここに7個のブロックが存在するとします。このときのハノイの塔の成功回数は別表より19回となっています。これは始めに7個中の3個を他の棒に積み重ねます。このときは5本棒すべてが機能して5本棒のハノイの塔として扱うことが出来ますが、次に、残り4個のブロックを積み重ねるに当たっては一番小さいブロックがある一つの棒を使用不可能にしているため4個のブロックの移動は4本棒のハノイの塔と同じことになります。このように、5本棒のハノイの塔の中には4本棒のハノイの塔の特徴が現れてくるのです。
| 枚数(n) | 3本ハノイ | 4本ハノイ | 5本ハノイ | 一枚残 | 二枚残 | 三枚残 | 四枚残 | 五枚残 | 六枚残 | 七枚残 | 八枚残 | 九枚残 | 十枚残 |
| 1 | 1 | 1 | 1 | ||||||||||
| 2 | 3 | 3 | 3 | 3 | |||||||||
| 3 | 7 | 5 | 5 | 7 | 5 | ||||||||
| 4 | 15 | 9 | 7 | 11 | 9 | 7 | |||||||
| 5 | 31 | 13 | 11 | 19 | 13 | 11 | 11 | ||||||
| 6 | 63 | 17 | 15 | 27 | 17 | 15 | 15 | 15 | |||||
| 7 | 127 | 25 | 19 | 35 | 25 | 19 | 19 | 19 | 19 | ||||
| 8 | 255 | 33 | 23 | 51 | 33 | 27 | 23 | 23 | 23 | 27 | |||
| 9 | 511 | 41 | 27 | 67 | 41 | 35 | 31 | 35 | 39 | 43 | |||
| 10 | 1023 | 49 | 31 | 83 | 49 | 43 | 39 | 35 | 31 | 35 | 39 | 43 | |
| 11 | 2047 | 65 | 39 | 99 | 57 | 51 | 47 | 43 | 39 | 39 | 43 | 47 | 51 |
5本ハノイの最小手数の規則性
そしてn枚の4本ハノイの最小手数の数列{an}と、その階差数列{bn}は次のようになる。
{an}
1,3,5,7,11,15,19,23,27,31,39,47,55,63,71,79,87,95,103,111,127,143,159,175,191,207,223,239,255,271,287,303,319,335,351,383
{bn}
2,2,2,4,4,4,4,4,4,8,8,8,8,8,8,8,8,8,8,16,16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16, 16,32,・・・
2が3つ、4が6つ、8が10、16が15・・・
なにやら規則性が見えてきた・・・
さいごに
2000年の7月〜8月にかけて行った研究によって「4本ハノイ」の結果がまとまり、それを2000年9月1日の文化祭で発表しました。この結果は大変面白い結果でしたので、5本ハノイについても調べはじめました。最後の表は2000年12月ごろにできました。そして、2001年8月に文化祭にむけて5本ハノイについてのレポートを作りましたが、文化祭のために昨年の「4本ハノイ」とあわせて、作り直すことにしました。
トップへ 取れたての定理集へ 少年少女数学愛好会へ ホームへ
| SEO | [PR] 爆速!無料ブログ 無料ホームページ開設 無料ライブ放送 | ||
