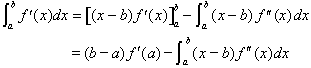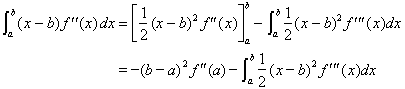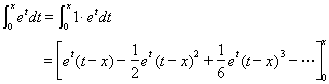�@�P�O���P�X���i�y�j�ɂ����ꂽ�T�[�N���̗l�q�����m�点���܂��B
���R���������̉�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���_�疾�i������ꍂ�Z�j
�@���Z�P�N�u���Ǝ��v�̉��K�œo�ꂷ����������̌���
![]()
�ɂ���a���w�ɒu�������Đ��������
![]()
![]() �c�c�@
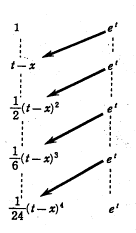
�c�c�@
���̎��𗘗p���ĂR��������![]() �c�c�A�������Ă݂悤�B
�c�c�A�������Ă݂悤�B
�@ �̍��ӂƔ�r����
![]() �@���Ȃ킿�@
�@���Ȃ킿�@![]()
����āA![]() �͂Q��������
�͂Q��������
![]()
�̉��ł���B![]() �Ȃ̂ŁA�Q��b,c�́A
�Ȃ̂ŁA�Q��b,c�́A![]() �ƂȂ�B�]���ćA�̍��ӂ́A
�ƂȂ�B�]���ćA�̍��ӂ́A
![]()
�ƈ�����������A�������̉���
![]()
![]()
![]()
�ƂȂ�B
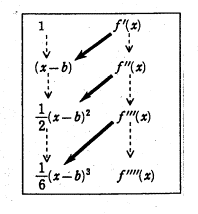
��![]() �̒��Ԃ����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���͌��@�p�i�y�č��Z�j
�̒��Ԃ����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���͌��@�p�i�y�č��Z�j
����w���w�̉˂����F�����ϕ��ƃe�[���[�W�J�@�@�@�@�@�@�@�@�@�@�@������j�i������O���Z�j
���P�v���[�̕��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�{���Y�i�Ԋ��k���Z�j
�@�e�B�R�u���[�G�̊ϑ��f�[�^��p���ăP�v���[�͒n���Ɖΐ��̌��]�̋O���ׂ����Ƃ͗L���ł��B�����藝�𗘗p���āA��r�I�ȒP�Ɂu�n���̌��]�͂قډ~�O���Ƃ݂Ȃ��Ă悢���A�ΐ��͑ȉ~�O���ł���v���Ƃ��Ǒ̌��ł��܂��B
�@�n���̌��]������365���A�ΐ��̌��]������678���ł��邱�Ƃ͊��ɂ킩���Ă��܂��B�܂��A�n������݂����z�̕����Ɖΐ��̕����̓e�B�R�̃f�[�^�ɂ���ė^�����Ă��܂��B
�@���z�r�ƒn���d�Ɖΐ��l���꒼���ɕ��ԁu�Ձv�̂���678����̑��z�Ɖΐ��̕����̃f�[�^�Ƃ����678����̃f�[�^���玟�̂��Ƃ��킩��܂��B
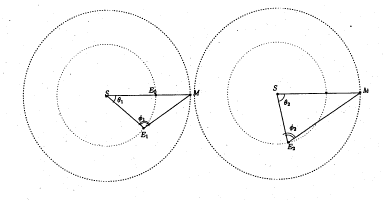 �@�}�̃Ƃƃӂ̓f�[�^����킩��܂��̂ŁA�����藝�ɂ��
�@�}�̃Ƃƃӂ̓f�[�^����킩��܂��̂ŁA�����藝�ɂ��
![]() �@�ƂȂ�̂Ł@
�@�ƂȂ�̂Ł@![]()
���킩��܂��B�����678����̃f�[�^���瓯�l��
![]()
���̂悤�ɂ��Ēn���O����̓_![]() �����܂�ƁA�n���̋O���Ɖ^�s���x���r�l����Ƃ������̂Ƃ��Čv�Z����܂��B���̂��Ƃ���A�n���̋O���͉~�Ƃ݂Ȃ��Ă悢���Ƃ�������܂��B
�����܂�ƁA�n���̋O���Ɖ^�s���x���r�l����Ƃ������̂Ƃ��Čv�Z����܂��B���̂��Ƃ���A�n���̋O���͉~�Ƃ݂Ȃ��Ă悢���Ƃ�������܂��B
�@
�����̒����E�p�x�E�ʐρE�̐ρ@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�{���Y�i�Ԋ��k���Z�j
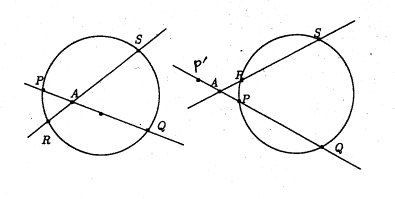 �@�����̒藝�̒��Œʏ�͋t�����藧���Ȃ��ꍇ�ɂ��A���̒������l���邱�Ƃɂ���āA�t�����藧�悤�ɂ��邱�Ƃ��ł��܂��B�Ⴆ�A�u���ׂ��̒藝�v�ł́A�_�`��ʂ�Q�̒�����ɂQ�_�o�A�p����тq�A�r������Ƃ�
�@�����̒藝�̒��Œʏ�͋t�����藧���Ȃ��ꍇ�ɂ��A���̒������l���邱�Ƃɂ���āA�t�����藧�悤�ɂ��邱�Ƃ��ł��܂��B�Ⴆ�A�u���ׂ��̒藝�v�ł́A�_�`��ʂ�Q�̒�����ɂQ�_�o�A�p����тq�A�r������Ƃ�
�w�o�A�p�A�q�A�r������~����ɂ�����AP�E�`�p���`�q�E�`�r�x
���̒藝�̋t�͐��藧���Ȃ��B�e�}�ŁA�~��ɂ���_�o�ɑ��āA�_�`�Ɋւ��đΏ̓_�o�f���Ƃ�ƁA���̓_�Ɋւ��Ă��W���͐��藧���Ă���̂ɂ�������炸�A���̂S�_�͓���~����ɂȂ��B
�@�������A�����`�o�A�`�p�A�`�q�A�`�r�Ɍ������l�����̒��������e����A
�_�`���~�̓����ɂ���Ƃ��́A�`�o�E�`�p���O�A�`�q�E�`�r���O
�_�`���~�̊O���ɂ���Ƃ��́A�`�o�E�`�p���O�A�`�q�E�`�r���O
�ƂȂ�t�����藧�B
�@���l�̂��Ƃ́A�����藝��l���E�X�̒藝�E�`�F�o�̒藝�ɂ��Ă�������B�܂��A���̊p�����e����A�~���p�̒藝�ɂ��Ă���ʁA�D�ʂɂ�����炸����I�ɑ����邱�Ƃ��ł���B����ɁA���̖ʐς╉�̑̐ς����e����A���_�n�Ɠ_�`�A�a�ɑ��Ăn�`�C�n�a���Q�ӂƂ��镽�s�l�ӌ`�̖ʐς����߂鎮�⌴�_�n�Ƌ�Ԃ̓_�`�A�a�A�b�ɑ��Ăn�`�A�n�a�A�n�b���R�ӂƂ��镽�s�U�ʑ̂̑̐ς����߂鎮������I�ɏ������Ƃ��ł���B
�@���̕��̒����A�ʐρA�̐ς͐��w����Ŏ��ɑ�Ȗ������͂����Ǝv����B
�������̔{�ϖ��Ɛ܂莆�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ɓ�����i���ڍ��Z�j
�@�܂莆�ɂ���}�@�́A��K�ƃR���p�X�ɂ���}�̂ł��Ȃ��^�C�v�̍�}���\�ł��邱�Ƃ͈ȑO����m���Ă����B
�@�����̔{�ϖ��̐܂莆�ɂ���@���Љ�悤�B
�@�܂��A�����`���R��������B
�@��̐}�ɂ����āA![]() �Ƃ���ƁA
�Ƃ���ƁA![]() �ŁA���p�O�p�`
�ŁA���p�O�p�`![]() �ɒ��ڂ��A
�ɒ��ڂ��A![]() ��
��![]() �͑����ł��邱�Ƃ���
�͑����ł��邱�Ƃ���
�@�@
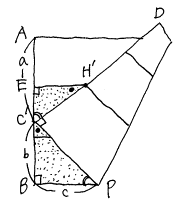
![]() �@���Ȃ킿�@
�@���Ȃ킿�@![]()
��������B�܂�A![]() �ƂȂ�̂ł���B
�ƂȂ�̂ł���B