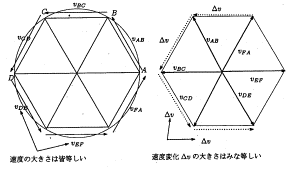
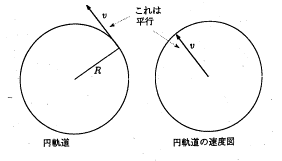
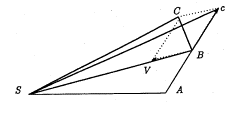
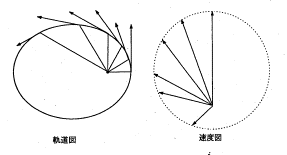
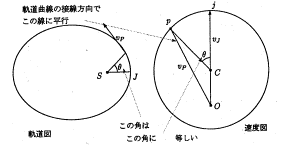
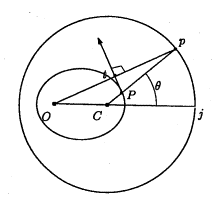
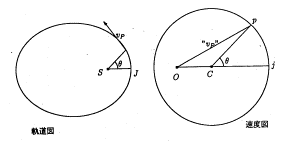
�P�Q�����̘b�肩��
�@�P�Q���P�S���i�y�j�ɂ����ꂽ�T�[�N���̗l�q�����m�点���܂��B
�������ւ̎��Ƃł��Ȃ��������Ƃɂ����@�@�@�@�@�@�@�@�@�@������j�i�����O���j�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�P�@�����J���u�����܂�������v
�@�t�B�{�i�b�`�^����́A�a�������{���܂��t�B�{�i�b�`�^����ɂȂ�̂�
�u�t�B�{�i�b�`�^����̓x�N�g����Ԃ��Ȃ��v
�Ƃ����܂��B���āA
�t�B�{�i�b�`����@![]()
�����J���@�@�@![]()
�Ƃ��āA
![]()
�Ƃ���A����̓t�B�{�i�b�`�^����̂P�������Ȃ̂�![]() ���܂��t�B�{�i�b�`�^����ƂȂ�܂����A�܂�������̓��䐔��ł�����܂��B
���܂��t�B�{�i�b�`�^����ƂȂ�܂����A�܂�������̓��䐔��ł�����܂��B
����![]() ���u�����܂�������v�Ɩ����������B
���u�����܂�������v�Ɩ����������B
��̓I�ɂ́A
![]()
�@�Q�@�t�B�{�i�b�`���ƃ��[�N���b�h�̌ݏ��@
�@�t�B�{�i�b�`����ׂ̗荇���Q�����l����B�Ⴆ�A55��89�Ƃ���B���̂Q���̍ő���͉��ł��傤���H
![]()
![]()
�u�t�B�{�i�b�`����ׂ̗荇���Q���݂͌��ɑf�v
�@�R�@�p�X�J���̎O�p�`�ƂQ���藝
�����藧���܂��B��ʂɁA�p�X�J���̎O�p�`�̂��i�̕����![]() �Ƃ���ƁA
�Ƃ���ƁA
![]()
�Ȃ̂ŁA![]() �͏����P�A����1+x�̓��䐔���
�͏����P�A����1+x�̓��䐔���
![]()
�ł��邱�Ƃ��킩��܂����B�܂�A�Q���W���ɂȂ��Ă��邱�Ƃ��킩�����B
�@�S�@�p�X�J���̎O�p�`�̉��̐���̘a
��������B
���j���[�g���̍l���������@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�{���Y�i�Ԋ��k���Z�j
���u���ϕ���ڂŌ��悤�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ɓ�����i���ڍ��Z�j
�@�P�Q���ɂU�l�̐��k��ɐ��w�V�ł̒u���ϕ��̎��Ƃ����Ƃ��̓��e�̏Љ�B
��ϕ�![]() ���l���悤�B�����
���l���悤�B�����![]() �ƒu�����Ă݂�ƁB
�ƒu�����Ă݂�ƁB
![]() �@���@
�@���@![]() �@���Ȃ킿�@
�@���Ȃ킿�@![]() �@�����
�@�����
�@![]()
![]() �@���@�@�O�@���@�P�@�@�@�@���̒�ϕ��̒l�h�͉��}���̖Ԋ|���̖ʐςɂȂ�B
�@���@�@�O�@���@�P�@�@�@�@���̒�ϕ��̒l�h�͉��}���̖Ԋ|���̖ʐςɂȂ�B
![]() �@�@�@�@�@�@�@�@�@�@�@�@�@���̂Q�̐}���r����ƁA�u���������́A����������−�Q�������s��
�@�@�@�@�@�@�@�@�@�@�@�@�@���̂Q�̐}���r����ƁA�u���������́A����������−�Q�������s��
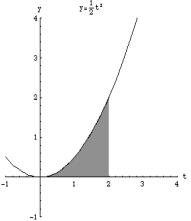
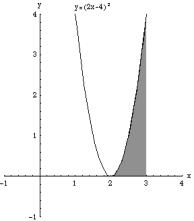 �@���@�@�O�@���@�Q�@�@�@�@�����A����ɂ��������ɂQ�{�Ɋg�債�A����������
�@���@�@�O�@���@�Q�@�@�@�@�����A����ɂ��������ɂQ�{�Ɋg�債�A����������![]() �ɏk�����Ă��邱�Ƃ��킩��܂��B����āA���̂Q�̖ʐς͓������Ȃ邱�Ƃ��킩��܂��B
�ɏk�����Ă��邱�Ƃ��킩��܂��B����āA���̂Q�̖ʐς͓������Ȃ邱�Ƃ��킩��܂��B
���̂悤���āA��ϕ�����![]() �̂Ƃ��̒�ϕ�
�̂Ƃ��̒�ϕ�
![]()
�ł́A![]() �ƒu�����邱�Ƃɂ���āA�ϕ������Ԃ�
�ƒu�����邱�Ƃɂ���āA�ϕ������Ԃ�![]() ����
����![]() �ɂ����A��Ԃ̕��͂��{�Ɋg��i�k���j����B
�ɂ����A��Ԃ̕��͂��{�Ɋg��i�k���j����B
�܂��A![]() �ƒu�����邱�Ƃɂ���āA��ϕ����́A
�ƒu�����邱�Ƃɂ���āA��ϕ����́A![]() ����
����![]() �ɂ����A���̒l��
�ɂ����A���̒l��![]() �{�ɏk���i�g��j����B�ϕ��̋�Ԃ͂��{�ɂȂ�A����A��ϕ����̒l��
�{�ɏk���i�g��j����B�ϕ��̋�Ԃ͂��{�ɂȂ�A����A��ϕ����̒l��![]() �{�ɂȂ�̂Œ�ϕ��̒l�͕s�ςɂȂ�̂ł���B
�{�ɂȂ�̂Œ�ϕ��̒l�͕s�ςɂȂ�̂ł���B
�@�ł́A��ϕ�����![]() �̂Ƃ��͂ǂ��l������悤�����낤���H���̂��߂ɂ́A��ϕ��̒�`���Ȃ킿���[�}���ϕ��i�敪���ϖ@�j�ɗ����Ԃ��čl�@���Ȃ���Ȃ�Ȃ��B
�̂Ƃ��͂ǂ��l������悤�����낤���H���̂��߂ɂ́A��ϕ��̒�`���Ȃ킿���[�}���ϕ��i�敪���ϖ@�j�ɗ����Ԃ��čl�@���Ȃ���Ȃ�Ȃ��B
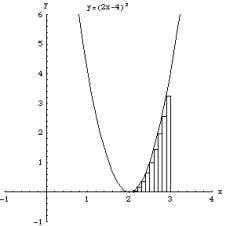 �@��ϕ�
�@��ϕ�![]() ���敪���ϖ@�ōl���悤�B�ϕ��̋��
���敪���ϖ@�ōl���悤�B�ϕ��̋��![]() ��10�������A�������11�̕��_
��10�������A�������11�̕��_![]() �����B����ɑΉ������ϕ����̒l
�����B����ɑΉ������ϕ����̒l![]() �Œ����`������A���̘a���v�Z���A���̒�ϕ��̋ߎ��l�����߂�B���R�A�������鐔���傫���Ȃ�قNjߎ��l�̒��x�͗ǂ��Ȃ�B
�Œ����`������A���̘a���v�Z���A���̒�ϕ��̋ߎ��l�����߂�B���R�A�������鐔���傫���Ȃ�قNjߎ��l�̒��x�͗ǂ��Ȃ�B
�@���ɁA��̒�ϕ���![]() �ƒu������
�ƒu������![]() ���敪���ϖ@�ōl���悤�B�u��
���敪���ϖ@�ōl���悤�B�u��![]() �Ō��܂�
�Ō��܂�![]() ��11�̕��_�����B����ɑΉ������ϕ����̒l
��11�̕��_�����B����ɑΉ������ϕ����̒l![]() �Œ����`������A���̘a���v�Z���A���̒�ϕ��̋ߎ��l�����߂�B��������R�A�������鐔���傫���Ȃ�قNjߎ��l�̒��x�͗ǂ��Ȃ�B
�Œ����`������A���̘a���v�Z���A���̒�ϕ��̋ߎ��l�����߂�B��������R�A�������鐔���傫���Ȃ�قNjߎ��l�̒��x�͗ǂ��Ȃ�B
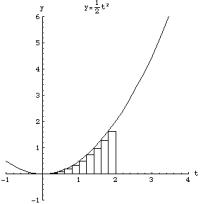 �@�Ƃ���ŁA��ō��ꂽ�����`
�@�Ƃ���ŁA��ō��ꂽ�����`![]() �Ƃ����u�����č��ꂽ�����`
�Ƃ����u�����č��ꂽ�����`![]() ���r����ƁA�S�Ă̑Ή����钷���`�ɂ���
���r����ƁA�S�Ă̑Ή����钷���`�ɂ���
�����`�̉����Q�{�A�c��![]()
�ł���̂ŁB
![]()
�����
![]()
���ꂩ��A�Q�̒�ϕ��̒l�͓��������Ƃ��킩��B