２月例会の話題から

 

　２月１日（土）にもたれたサークルの様子をお知らせします。

 

 

●２次関数の問題づくり他　　　　　　　　　　　　　　　増島高敬（和光学園・自由の森学園）　　　　　　　　　　　　　　　　　　　　　　　

　１　２次関数の問題作りについて

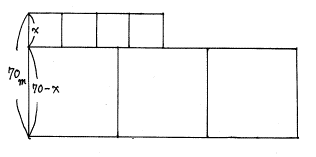
　夏休み自主学習問題を幾つか紹介します。まず「商品の値上げと売り上げの最大値」です。

『うちの雑貨屋さんでは手作りのぬいぐるみを売っています。クマのぬいぐるみは１つ作るのに200円かかり、400円で売っています。１日に60体売れています。もうけを最大にするにはいくらで売ればいいでしょうか？過去のデータによると、10円の値上げごとに５体ずつ売れる数がへるそうです。』

　ｘ円の値上げに対するもうけの金額ｙは

となる。この場合はすなわち360円で売ったときにもうけが最大になる。ところで、ｘ円の値上げに対する売り上げの金額ｙは

となり、この場合もすなわち360円で売ったときにもうけが最大になる。ところが、ぬいぐるみの原価が300円になると、売り上げの最大になるときは上と同じであるが、もうけの金額ｙは

となり、すなわち410円で売ったときもうけが最大になる。このように、「売り上げの最大になるとき」と「もうけが最大になるとき」が違うこともある。

　一般に、ｘ円の値上げに対する「売り上げ」または「もうけ」の金額ｙは

という形になり、

のときは、値上げしたほうが有利

のときは、値下げしたほうが有利

となります。次に「土地の切り売りの問題」です。

『あるおじいさんが間口70ｍの広い土地をもっているのですが、その一部を正方形の区画７つ分売ろうとしています。しかし、より多くの土地を孫の遊び場として残したいため売る面積をできるだけ小さくしたいのです。そのためには間口70ｍをどのように区切ればいいでしょうか？』

　図のように１つの正方形の一辺をｘとすると、売る土地の面積ｙは、

となる。この場合はのときがｙが最小になるが、この結果を図示すると売る土地が長方形状になってしまう。なぜか嬉しい？結果である。

 

 

 

　２　微分の問題作り

　　微分らしい問題は、積分の問題に比べてあまりない。そこで幾つか作ってみた。そこで「改札口の問題」から

『あるターミナルえきでは朝８時からラッシュアワーに入り９時までの間に36000人の通勤客が改札口を通ります。８時から８時ｘ分までの間に改札口を通る人数は人で９時にはピークとなります。

１）     改札口を通る人の流れは平均して毎分何人ですか？

２）     ピーク時である９時に客をスムーズに流すためには毎分50人通すことのできる自動改札機が少なくとも何台必要ですか？』

８時から８時ｘ分までの間に改札口を通る人数を

人

とすると、９時の１分あたりの通過人数は

人

であるので、自動改札機は、台必要になる。流量と流率のテーマはやはりひかれるものがある。

　３　瞬間の速度を求める　この車はスピード違反？

　高１のクラスで『瞬間速度は平均速度の極限という「迂回作戦」により求められることを理解する』授業の実践の紹介。ご存じファインマン物理学の脚色したもの。実に面白い。

 

 

●電卓の働き他　　　　　　　　　　　　　　　　　　　　　　　　　　宮本次郎（花巻北高校）

　１　電卓の働き

　電卓の中で何が行われているのか推理しようということで、電卓の種々の実験をしてみた。

実験１：電卓で２　＋　＝　とキーをたたくとどうなるのでしょう？

なんと電卓によって結果が違うのです。100円ショップで買った電卓では、表示は

　　　　　　　２　２　２

となりました。では次の実験

実験２：電卓で２　＋　＝　＝　とキーをたたくとどうなるでしょう？

100円電卓では、表示は

　　　　　　　２　２　２　４

となりました。ということは、電卓の内部ではこの「２」という数字や「＋」という演算を覚えて、処理しているらしい。では次の実験

実験３：電卓で１　＋　２　＝　＝　とキーをたたくとどうなるのでしょう？

100円電卓では、表示は
　　　　　　　１　１　２　３　５

となりました。どうやら電卓はＡ＋Ｂの「＋Ｂ」の部分を覚えていて、「＝」が押されるたびに、もう一つの数に「＋Ｂ」をするようになっているようである。

 

実験４：電卓で１　＋　２　＋　＝　＝　と誤ってキーをたたいたらどうなるのでしょう？

　　　　　　　１　１　２　３　５　８

となりました、どうやら「＝」キーを押したときの内部処理と「＋」キーを押したときの内部処理が違うようである。そこで、Ｊくんは次のように推理した。

　（１）最初は記憶場所ＡもＢも内容がクリアされている。

　（２）数の入力があるとＢに格納される。

　（３）演算キー「＋」が押されるとＢの内容をＡの内容に加えてＡに書き込み、その際古いＡの内

　　　容はＢに転送される。

　（４）計算実行キー「＝」が押されるとＢの内容をＡの内容に加えてＡに書き込む。（Ａの古い内　

　　　　容はＢに転送されない）

　100円電卓でもレジスターやアキュムレーターなどのマシンぽいことを考えることができるのですね。

 

　２　加速度をめぐって

　数研の教科通信「サイエンスネット」１１月号に掲載された内容のリプリント。各種の加速度計を作成して新幹線等で実験した内容の報告です。

 

　３　ガウスの海

　昨年１１月の東北ＡＭＩ研究大会で出会った仙台二高の生徒達が作った数学研究会誌「アレフヌル」の中にあった「ガウスの海」の紹介。ガウスの海という複素数平面上を航海する船長の話題を楽しくてんかいしている。

 

 

●無理数の小数展開を目で見よう　　　　　　　　　　　　　　　　　　下河原英（軽米高校）

　無理数を小数展開すると、

1.414213562373095048801688724209698078569671875376948073176679737990732478462107038850…

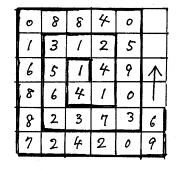となるが、この各位の数を将棋盤状のます目に螺旋を描くように配置する。そして、０〜９までの数字に対応する色を塗っていくとどのような模様ができるか。無理数の場合はランダムなパターンしか出てこないが、有理数ではいろいろなパターンが浮かび上がる。

　このようなワークシートをエクセルで作ったものの紹介でした。なんと、Ａ３版の印刷できるカラープリンターまで持ち込んで実況中継風発表でした。

　「ラウムの螺旋」につづいてのヒットになるかも？

 

 

 

 

 

 

 

 

●大学数学の架け橋　　　　　　　　　　　　　　　　　　　　下町壽男・亀掛川君（盛岡三高）

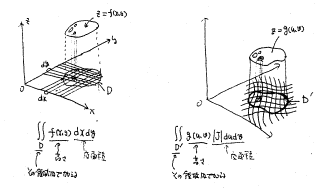　東北大工学部のＡＯ入試に合格した三高の亀掛川君に大学から数学のテキストが送られてきたそうです。そのテキストを勉強してレポートを出さなければならないのだそうです。このテキストを見てびっくり！多変数の微積分学が中心で、偏微分・全微分や２重積分やヤコービアンを使った置換積分などがばんばん登場してきます。これを独力で学ぶのは至難の技でしょうが、なんと亀掛川君はどんどん消化しているようです。でも要所要所でのサポートは必要で、下町先生が面倒を見ているとのことです。

　下町先生の「全微分可能」と「ヤコービアン」のサポートのプリント（何とカラーコピー）の説明でした。

 

　平面の方程式を学んでいない者に全微分をわかってもらったり、１次変換を学んでいない者にヤコービアンをわかってもらうのは大変だと思いますが、さすがシモマックは綺麗は絵の力で乗り越えていました。

 

　そして、飛び入りで亀掛川君の発表があり、正７角形の辺ａと第１対角線ｂ、第２対角線ｃとのあいだに、

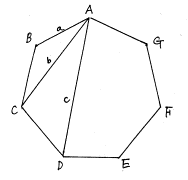
という関係があるという問題を投げかけられたのです。彼は、方程式の解が正７角形の頂点を表すことから。相反方程式から３次方程式を導き云々とやろうとしていたみたいです。サークルでは、いろいろなアイデアが提出されましたが結構計算がややこしい部分があったりしたので宿題にしてしまいました。実は初等幾何的な解法が一番楽であることが後からわかってきました。この辺のやり取りについては、数学教室をみてください。現役の高校生の飛び入りで多いに盛り上がりました。

 

 

 

●計算は合理化記号で　　　　　　　　　　　　　　　　　　　　　　　和田年央（秋田無量塾）

　久しぶりの和田氏の登場。Ａ４版７ページにギッシリ難しげな記号が並んでいる。今回はどうやら逆三角関数と逆双曲線関数にかかわる話題のようである。

　和田氏曰く「三角関数・双曲線関数および逆三角関数・逆双曲線関数はすべて『非（hi）線形』であり、定数倍ｉの出入りとそのとき脱着するハイパーのｈとはペア（ｈ、ｉ）で変形されます。」

「等がわかっていれば、の結果から容易にの結果を導けます。」

　よって、公式として掲げるなら２つをパラレルに記した方が合理的なそうです。

　同様にして、次の２つの公式が掲げられる。

　ハイパーボリックにかけては和田氏の右に出るものはないという印象であった。

 

 

 

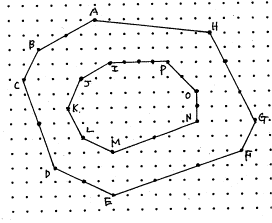
●ピックの定理の授業　　　　　　　　　　　　　　　　　　　　　　　　伊藤潤一（平舘高校）

　昨年の１２月に３年家計科学科でやった授業の報告。ピックの定理とは「平面格子を結んでできる多角形の面積をＳとする。このとき、内部の点の数がａ、境界上の点の数がｂであれば、が成り立つ。」というもの。実際にやってみると、100を超えると内部の点を数えるのがかなり大変であった。

　ピックの定理を使って格子点を結んでできるいろいろな多角形の面積を求める問題を授業で取り組んだ。ところが図のように中に穴がある（ドーナツ状の）図形の面積を求める際、生徒は２通りの解き方をした。

　一つは、外側の多角形の面積と内側の多角形の面積をそれぞれピックの定理で求めて引き算して求める方法である。もう一つは穴の部分は外側とみなして、ドーナツ状の部分にピックの定理を使って求める方法である。

　ところが、実際に計算してみると。２つの方法で求めた面積は１だけ違うのである。

　穴が１つあるタイプの面積は、となることがわかった。

　一般に、穴がｐ個あるタイプの面積は、となることがわかる。ピックの定理は、位相不変量を含んだ定理だったのである。