�f03�m�˃T�[�N���P�Q�����̈ē�
�@���R�������܂Ŋ���ł��B���悢�悤�~������Ă��܂����B�T�[�N������̊F�l�ɂ͎t���̌�A���ς�炸���C�Ő��w���Ă���ł��傤���B�P�P���Q�X���A�R�O���̂`�l�h���k���̓T�[�N������̊F�l�̋��͂ɂ��听���̂����ɏI���ł��܂����B����ꂳ�܂ł����B���āA�x�ފԂ��Ȃ����N�Ō�̓m�˃T�[�N���̂P�Q���������̓����ł����܂��B�Z�������ł��傤���A�ȂɂƂ��s�������ĎQ����������悤���肢�������܂��B
�@�Ȃ��A���I����ɂ����̌������Łg�]�N��h�����\��ł��̂ŁA������̎Q������낵�����肢���܂��B
�L
�P�@���@ ���@�P�Q���P�R���i�y�j�����S�F�O�O�`�V�F�R�O
�Q�@��@ ���@����w����w�����{�R�������i�S�O�V���j
�@�@�@�@�@ �@ tel 019-621-6539 fax
019-621-6543
�R�@�T�[�N����� ���H���|�[�g���\�E����
�@�@�@�@�@�@
���w�G�k
�C���t�H���[�V����
�� �P�P���Q�X���i�y�j�A�R�O���i���j����w����w���Ɗ����z�e���ł`�l�h�̓��k��������A�����E�n�a�Ŗ�V�O�l�A�����E���k��V�O�l�A�����Q�O�l�̎Q���ő吷���ł����B����̖ڋʂł������������Ƃ͏��w�Z�F�H�c�搶�i�����j�A���w�Z�F�����搶�i�����j�A�����č��Z�͉䓙���T�[�N���̃z�[�v���͌��搶�Ƃ����C����ƂĂ��悢���Ƃ��ł��܂����B

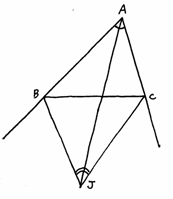
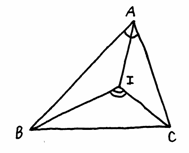
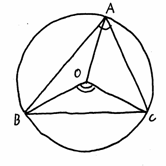
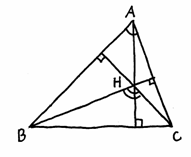
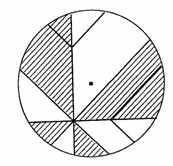
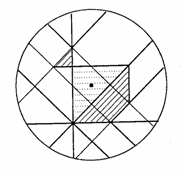
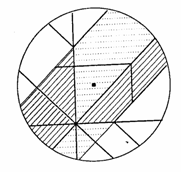
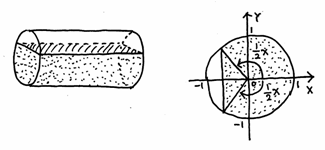
���ȉ�ł́A�����搶�́u�ϕ��̓����v�A���q�搶�́u�O�p�`�̌ܐS�v�A���_�搶�́u���ς̊w�I�Ӗ��v�A�{�{�搶�́u���[���[�̉�]�́v�Ɖ����搶�̃r�f�I�u���k�ƂƂ��ɍl����i�w�Z�ɂ�������Ɓv�̔��\������܂����B


����ɉ����搶�̓|�X�^�[�u

�ތl�̑̌��̘b�Ȃ̂Ɂu�Ȃ����w���w�Ԃ̂��H�v�Ƃ����₢�����̈�̉ɂȂ��Ă���Ƃ����B���N���N����悤�Ȓ����ł������B���N�x�̓��k����
�� �P�P���V���i���j��T�Q�k�n��Z���E���w���猤���i���j�������O���ł����ꉺ���搶���܂��܂����J���ƁB����͕��f�����ʂ�ɂ����g���ƂȂ��t���N�^���h�B�O���̐��w�����̌������Ƃ̑��҂łƂĂ��y�������Ƃł����B�܂��A�����搶�┵���搶���������\�I�m�˃T�[�N���������ԍv�����Ă��܂��ˁ[�B
�� �P�P���P�S���i���j�`�P�T���i�y�j�Ԋ�����Ŋ�荂���g�����W��i���ȕʁj��������A���w���ȉ�͎Q���҂Q�O������Q���B���������\���|�[�g���P�O�{�B���܂��Ɏ��̎Q���҂��ڗ��ƂĂ����C���鋳���W��ł����B���N�x�̓����g�����ɂ́A���_�搶���u�����������v�̃��|�[�g�ŎQ�����܂��B�i��҂̐쑺�搶�Ƃ��ǂ��撣���Ă��������B
�� �P���V���i�y�j�A�W���i���j�Ɋ�薯�����~�̏W��\�肳��Ă��܂��B����̏W��͂Ȃ�ƋC��̂悤�ł��B�����������ł������̒��ł͉��g�ŊC�̍K���L�x�ȂƂ���ł��B��������Q�����Ă��炦����Ǝv���܂��B�ڂ����v���͌�قǏo��͂��ł��B
�� ��D���̋{�{�搶�Ɖ����搶�̃z�[���y�[�W�B�{�{�搶�̃z�[���y�[�W�̒��ɓm�˃T�[�N���̃R�[�i�[������܂��B�F����̂����Ă݂悤�B
�@�@�@�����搶��HP�@�@http://www5b.biglobe.ne.jp/~simomac/
�@�@�@�@�{�{�搶��HP�@�@http://homepage1.nifty.com./toretate/
�P�O�����Part2�̗l�q
�@�Q�N���̂`�g�Ƃa�g�̐��w�U�̎O�p���̉��@�藝�̉��p�Ƃ��ĎO�p���\���쐬�������Ƃ�ł��B�P�������݂̕\�͂�����Ƌꂵ���̂ŏ�����U�ʂ܂ł̃T�C���E�R�T�C���̂R�������݂̕\������B
�@�܂��A�O���A�X�O���A�R�O���A�S�T���A�U�O���A�P�T���ƂV�T���̒l�͂��܂܂Ŏ��Ƃŋ��߂������l�����Ƃɓd����g���Ă���ŊȒP�ɋ��߂���B����łƂ肠�����P�T�������݂̃T�C���E�R�T�C���̕\���ł����B�P�T�������݂��ׂ��������݂̕\��ɂ́A���̊p�x�̐��m�Ȓl�����߂Ȃ���Ȃ�Ȃ��B�����ŁA���܊p�`�̂P�ӂƑΊp���̔䂪���߂��A���ꂩ�璼���ɃR�T�C���̂R�U���̒l�����߂���B���̂R�U���̃R�T�C���̒l�̔�������ɂ��ĉ��@�藝����g���ĂR�������݂̎O�p���̕\�������̂ł���B
�@�R�T�C���R�U���̒l![]() ��d��Ōv�Z�����
��d��Ōv�Z�����
![]()
�����܂�B�T�C���R�U����R�T�C���T�S���́A�O�p���̑��݊W���g���ċ��߂�B
�@���̂R�U���̃T�C���E�R�T�C���̒l���g���ĉ��@�藝�łU���̃T�C���E�R�T�C���̒l�����߂�B
![]()
�@�P�Q���̃T�C���E�R�T�C���̒l�����߂�悤�B
![]()
![]()
��͍��܂ł̒l����ɁA���@�藝�⑊�݊W�A�]�p�̌�����p���ēd�����g���ĎO�p���\���ǂ�ǂ߂Ă����悢�̂ł���B
�@�O�p���\����������A�Ȃ�Ƃ������Ȃ��������𖡂키���Ƃ��ł���B�i�قƂ�ǂ̐��k�͎��͂Ŋ��������邱�Ƃ��ł����B