’04杜陵サークル4月例会の案内
暖かい日、寒い日いろいろですが桜の便りが聞こえる季節になりました。年度末の忙しい中でサークル会員の皆様お元気でお過ごしでしょうか。きっと新年度を間近に控えて、来年の授業の構想を練っていることでしょう。さて、杜陵サークルの4月例会を次の日程でもちます。忙しい中でしょうが、なにとぞ都合をつけて参加くださるようお願いいたします。
なお、例会終了後にいつもの月見亭で“プレ花見の会”をもつ予定ですので、こちらの参加もよろしくお願いします。
記
1 日 時 4月3日(土)pm4:00~7:30
2 場 所 岩手大学教育学部小宮山研究室(407号)
tel 019-621-6539 fax 019-621-6543
3 サークル例会 実践レポート発表・検討
数学雑談
インフォメーション
● 3月13日(土)サークル会員の川村先生がついに華燭の典を挙げられました。媒酌人はなんと小宮山先生ご夫妻。サークルからもたくさん参加し「2人のバイオリズムによる相性度」「2人のモーフィングによる子ども予測」「不思議なかけ算による2人の深い結びつきの証明」「フーリエ変換でハッピーハッピー」など杜陵サークルワールドを展開。披露宴会場の人たちに深い印象(なんだ、あの集団は!)を与えました。また、川村先生自作の次々と無限展開できる「Welcome to our Wedding Reception」のカードも素晴らしいものでした。披露宴の後はそのまま終わるはずはなく2次会、3次会……と延々と続き、無限大に発散。お疲れさま!
● 3月27日(土)、28日(日)に「豊かな数学を楽しく」というテーマで信州・上諏訪温泉でAMIの全国高校研究集会がもたれます。いまのところ杜陵サークルからも宮本先生、伊藤先生、下河原先生が参加するとのこと。今回も楽しい集会になりそうです。多分その様子は4月例会で聞けると思います。
● 今年度の杜陵サークルの会員の人事異動は、わかっているところで、伊藤先生が盛岡北高校に、宮本先生が釜石南高校に、下町先生が花巻北高校に、鳩岡先生が一戸高校にというところです。新任地での活躍が楽しみですね。
● 絶好調の宮本先生と下町先生のホームページ。宮本先生のホームページの中に杜陵サークルのコーナーがあります。皆さんのぞいてみよう。
下町先生のHP http://www5b.biglobe.ne.jp/~simomac/
宮本先生のHP http://homepage1.nifty.com./toretate/
2月例会の様子
小数の連分数表示と同様に関数の連分数式表示を考えてみよう。与えられた関数を
![]()
とする。この関数を
![]()
と連分数に変形するには、与えられた関数の逆数のべき展開をたくさん計算しなければならない。しかし、この方法は結構大変な計算になる。もっと簡便な方法はないだろうか?
べき級数を効率よく連分数式に変換する方法は、20世紀中頃スイスのルティスハウザー(Hans Ruthishauser)が発案したという。この「商差法」で
![]()
を連分数式に変換してみよう。まず、初めに0の列を書き、次の列に![]() を書く。あとは、下のように①、②、③、④に配置された数に対して、④=①+②−③で次の列を計算し、その次の列は④=①×②÷③計算するのである。そして、この計算を交互に繰り返すのである。
を書く。あとは、下のように①、②、③、④に配置された数に対して、④=①+②−③で次の列を計算し、その次の列は④=①×②÷③計算するのである。そして、この計算を交互に繰り返すのである。
③
① ④
②
0
![]()
0 ![]()
![]()
![]()
0 ![]()
![]()
![]()
![]()
![]()
0 ![]()
![]()
![]()
![]()
![]()
![]()
0 ![]()
![]()
![]()
![]()
0 ![]()
![]()
0
これより
![]()
が得られる。連分数展開の途中で切ると、近似分数関数が得られる。この近似は、べき展開による近似よりずっと精度のよい近似式になる。例えば、
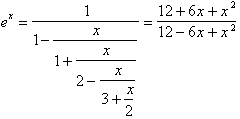 (4次近似)
(4次近似)
●数の話~連載・総集編~ 小宮山晴夫(岩手大学)
①同値関係・類別 ②自然数 ③整数環 ④有理数体 ⑤実数体 ⑥複素数体 という構成です。読み直してみると、数の拡張の流れがわかってとてもおもしろかったです。ただ、存在記号![]() や全称記号
や全称記号![]() の説明がもう少し欲しかったと感じました。
の説明がもう少し欲しかったと感じました。