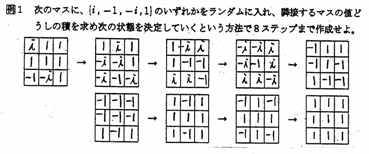
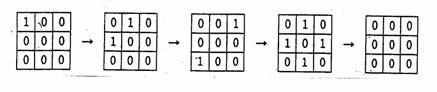
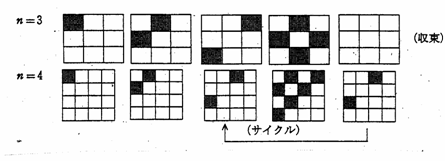
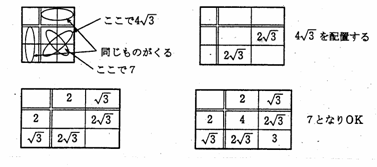
�f04�m�˃T�[�N���X�����̈ē�
�@
���[�̗������͂��̖ҏ��̉Ă����������v����قǂł��B���łɎR�̏�ł͍g�t���n�܂��Ă��܂��B�T�[�N������̊F�l���̏��H�����������������ł��傤���B���āA�m�˃T�[�N���̂X���������̓����ł����܂��B�X���Q�R���i�j�̊���w�̐��w���J�u���̒���ŁA������Ƌꂵ���ł��傤����낵�����肢���܂��B�Ȃ��A���I����ɂ����̌������Łg���H�����ł��h�����\��ł��̂ŁA������̎Q������낵�����肢���܂��B
�L
�P�@���@ ���@�X���Q�T���i���j�����S�F�O�O����V�F�R�O�܂�
�Q�@��@ ���@����w����w�����{�R�������i�S�O�V���j
�@�@�@�@�@ �@ tel 019-621-6539 fax
019-621-6543
�R�@�T�[�N����� ���H���|�[�g���\�E�����A������& ���w�G�k
�C���t�H���[�V����
�� �X���P�P���i�y�j�`�P�Q���i���j���s��
�� �X���P�U���i�j�`�P�V���i���j���̃z�e���V�[�K���A�}�����Ō����������w����̌�����������܂����B�T�[�N��������_�搶���u�ˉe�̐��w�v�̔��\�A�{�{�搶�������ǂŗ����̎d�������܂����B��������̃T�[�N�����̗l�q��������Ǝv���܂��B
�� �X���Q�R���i�j�P�R�F�O�O�`�P�U�F�R�O����w�l���Љ�w���P���ّ�P��c���Ŋ���w���J�u���u���w�̔�������̌����悤�v������܂��B���e�́A�u���w���w�Ԃ̂͂Ȃ����v�i�l�Ё@�吼�搶�j�A�_���p�Y������i����@���ؐ搶�j�̋�������u���ł��B�����Q�����}�̂悤�ł��̂ŁA���k��U���ĎQ�����Ă݂܂��B
�� �X������P�O���͍����g�̎x�������́g�G�߁h�ł��B�e�x���ł̐��w���ȉ��ϋɓI�ɐ���グ�ĂP�P���P�R���i�y�j�`�P�S���i���j�̋��ȕʌ������ɂȂ��Ă����������̂ł��B
�� �Q�O�O�U�N�̂`�l�h�S�������s�ψ���̒ʐM�u�l�R��l�̂Ԃ₫�v���n������܂����B�F�����͂Ő��̒ʐM����Ă悤�ł͂���܂��B���킹�āg���s�ψ���ւ̂��U���h���߁X�������ł��B
�� �Җ]�̐����n��̒��w�Z�T�[�N���u���������v�i���w�J��Ƃ����Ӗ��Ȃ̂������ł��j�����g�����܂����B����͂W���Q�V���i���j
�� �F�l�̂����͂ŁA�m�˃T�[�N�����|�[�g�W�Q�O�O�S���V�����Ɋ��s�ł��܂����B�E���m�l�Ɋ��߂Ă��炦��Ǝv���܂��B�T�[�N���ʐM�Q�O�O�R�`�Q�O�O�S�ƍ��킹�ĂP�O�O�O�~�Ƃ������荠�̉��i�ł��B
�� ��D���̋{�{�搶�Ɖ����搶�̃z�[���y�[�W�B�{�{�搶�̃z�[���y�[�W�̒��ɓm�˃T�[�N���̃R�[�i�[������܂��B�F����̂����Ă݂悤�B
�@�@�@�����搶��HP�@�@http://www5b.biglobe.ne.jp/~simomac/
�@�@�@�@�{�{�搶��HP�@�@http://homepage1.nifty.com./toretate/
�W�����̗l�q