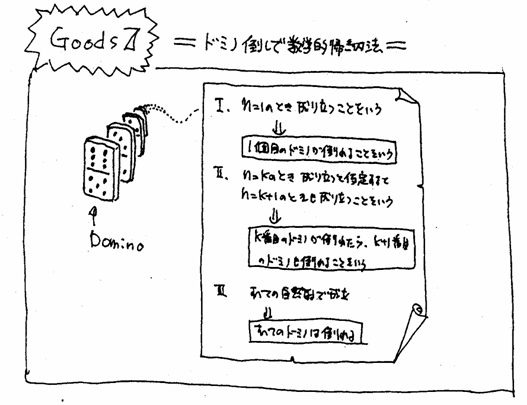
�@�f04�m�˃T�[�N���P�Q�����̈ē�
�@
�@���R�������܂Őቻ�ρA���܂ł��Ⴊ����Ă��Ă����������Ȃ������ɂȂ�܂����B�^�C���̌��������Ȃ���I�m�˃T�[�N���̉���̊F�l�A�����Ⓦ�k���Ȃǂ��܂��܂Ȍ�����Ŋ���ꂳ�܂ł��B���āA�m�˃T�[�N���̂P�Q���������̓����ł����܂��B�Ȃ��A���I����ɂ����̌������Łg���~���}�����h�����\��ł��̂ŁA������̎Q������낵�����肢���܂��B
�L
�P ���@ ���@�P�Q���S���i�y�j��.��. �S�F�O�O ���� �V�F�R�O �܂�
�Q�@ ��@ ���@����w����w�����{�R�������i�S�O�V���j
�@�@�@�@�@ �@ tel 019-621-6539
fax 019-621-6543
�R�@ �T�[�N�����
���H���|�[�g���\�E�����A������& ���w�G�k
�C���t�H���[�V����
�� �P�P���T���i���j�P�V�F�O�O�`����w���J�u���u���w�����Z�~�i�[�v��������A�u���f���ƕ������v�i��ʑ�F�����搶�j�Ɓu�]�E�ƃl�Y�~�F���U�G�l���M�[�������̂͂ǂ����H�v�i����F�ѓc�搶�j�̘b���܂����B�ǂ�����ƂĂ��������������e�ł������ѓc�搶�̚M���ނ̃T�C�Y�ƃG�l���M�[�̏���ʂ̖@�����ʔ��������ł��B���ΐ��̃O���t���g�����V�������H�̉\����������������̂ł����B�T�[�N������̊F�������������Q�����Ă��܂����B
�� �P�P���U���i�y�j�P�S�F�O�O�`����w����w���ő�R�����w�N���u��������܂�������̉Ԗk�̐��k���s���ŕs�Q���̂��ߐl���͏��Ȃ߂ł������A���k���́u�n�m�C�̓��ɂ��Ă̍l�@�v�̔��\������A�Ȃ��Ȃ��[���������̂ɂȂ�܂����B����͂P���Q�Q���̗\��ł��B
�� �P�P���P�R���i�y�j�`�P�S���i���j�q����z�e����ςŊ�荂���g�̋�����������܂����B�T�[�N���������́u�w�Z���琔�w�M���悤�v�i�Ԗk�F�����搶�j�A�u�R�����ŃO���t�𗝉����悤�v�i�Ԗk�F���搶�j�A�u���w�ɂ�����f�W�^�����ނ�p�������Ƃ̈��`�p�X�J���̎O�p�`�`�i��ˁF�����搶�j�A�u�����̐F�����ƃp�X�J���̎O�p�`�v�i�y�āF���͌��搶�j�A�u�Q�̐����̌�_�̋O�Ղɂ��āv�i����F���_�搶�j�A�u�s�����̊o���v�i���k�F�ɓ��搶�j�A�u���v���ނɊւ�����H�ƍl�@�v�i�����F�����~�搶�j�̂Ȃ�ƂV�l�����\�I�P���̎D�y�ł̑S�������ɂ͍����~�搶���s�����ƂɂȂ�܂����B�Ȃ��A�{�{�搶�́A
�� �P�P���Q�V���i�y�j�`�Q�W���i���j�ɂ`�l�h���k��
�� ��D���̋{�{�搶�Ɖ����搶�̃z�[���y�[�W�B�{�{�搶�̃z�[���y�[�W�̒��ɓm�˃T�[�N���̃R�[�i�[������܂��B�F����̂����Ă݂悤�B
�@�@�@�����搶��HP�@�@http://www5b.biglobe.ne.jp/~simomac/
�@�@�@�@�{�{�搶��HP�@�@http://homepage1.nifty.com./toretate/
�P�O�����̗l�q
�@�̂̐��w�T�i�P�X�V�O�N��j�̕s�����͂Q���s�����̑��ɁA�R���s�����A�����s�����A�����s�����A�O�p�s�����A�w���E�ΐ��s�����Ȃǂ����X�ɓo�ꂵ�Ă����B�i�����̍��Z���̓��x�������������̂��낤���H�j�������A���ꂼ��̕s�����͌ŗL�ȉ�@�������A������}�X�^�[����̂��ƂĂ���ς������B�i���k�����t���I�j�����ŁA�����̕s�����̓���I��@���҂ݏo���ꂽ�B�ȉ����̊T���������B
�@�E���̗�_�Ɛ��E���͈̔�
�@�@�@��![]() �̗�_�izero point�j�Ƃ́A������
�̗�_�izero point�j�Ƃ́A������![]() �����ł���B
�����ł���B
�@�@�@��![]() �̐��͈̔͂Ƃ́A�s����
�̐��͈̔͂Ƃ́A�s����![]() �ƂȂ�悤�Ȃ��͈̔͂ł���B
�ƂȂ�悤�Ȃ��͈̔͂ł���B
�@�@�@��![]() �̕��͈̔͂Ƃ́A�s����
�̕��͈̔͂Ƃ́A�s����![]() �ƂȂ�悤�Ȃ��͈̔͂ł���B
�ƂȂ�悤�Ȃ��͈̔͂ł���B
�@�@�@�@�s�����������Ƃ́A���̐��͈̔͂������͕��͈̔͂����߂邱�Ƃł���B
�@�E���̗�_�ƕ����̋K��
�@�@��_�̏d���x�ɂ���āA�אڂ����Ԃ̕��������܂�
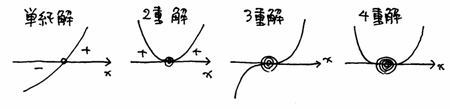
�@�@�@�i�P���j���A�R�d���A�T�d���A�c�@�ˁ@�ٕ���
�@�E�P���s�����̉�@�̃A���S���Y��
�@�@�@�C�j![]() �̌^�ɕό`����B
�̌^�ɕό`����B
�@�@�@�E�j���̗�_![]() �����߂�
�����߂�
�@�@�@�I�j�S�Ă̋�Ԃ̕����i�����j�����肷��
�@�u�R���s����![]() �������v
�������v
�@�i���j![]() �Ƃ���
�Ƃ���
 �@�@�@�i���̒�`��́A�����S�́j
�@�@�@�i���̒�`��́A�����S�́j
�@�@�@������![]() ��������
��������
�@�@�@�@![]()
�@�@�@�@![]() �i�Q�d���j
�i�Q�d���j
�@�@�@���![]()
�@�@�@�i�����̋K���ɂ��j![]()
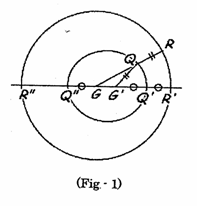
�@�P���s�����̉��͐�������̋�ԂɂȂ�i�P�����j���Q���s�����̉��͍��W���ʏ�̗̈�i�Q�����j�ɂȂ�B���̂��߂Q���̏ꍇ�́g�s�����������h���Ƃ́g�̈��}������h���ƂɂȂ�B����͑傫���ύX�_�ł���B
�@�E�Q�ϐ����̗�_�Ɛ��E���̈�
�@�@�@�Q�ϐ����̗�_�̏W���i���E���j�Ɗ��l�̕����̋K��
�@�@�@�@�P���ȋ��E��������Ɗ��̕������ς��
�@�@�@�@�Q�d�ɏd�Ȃ������E���͉����Ă����̕������ς��Ȃ�
�@�E�Q�ϐ����̗�_�Ɛ��̈�E���̈�
�@�@�@�Q�ϐ���![]() �̗�_�Ƃ͋��E��
�̗�_�Ƃ͋��E��![]() �ł���B
�ł���B
�@�@�@�Q�ϐ���![]() �̐��̈�Ƃ͕s����
�̐��̈�Ƃ͕s����![]() �ƂȂ�悤�ȓ_
�ƂȂ�悤�ȓ_![]() �̗̈�
�̗̈�
�@�@�@�Q�ϐ���![]() �̕��̈�Ƃ͕s����
�̕��̈�Ƃ͕s����![]() �ƂȂ�悤�ȓ_
�ƂȂ�悤�ȓ_![]() �̗̈�
�̗̈�
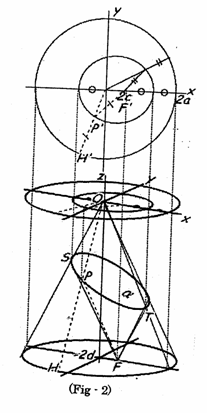
�@�@�@�Q���s�����������Ƃ́A�Q�ϐ����̐��̈�������͕��̈��}�����邱�Ƃł���B
�@�E�Q���s�����̉�@�̃A���S���Y��
�@�@�@�A�j��`������߂�i�m�F����j
�@�@�@�C�j![]() �̌^�ɕό`����B
�̌^�ɕό`����B
�@�@�@�E�j���E��![]() ��`��
��`��
�@�@�@�G�j�P�̗̈�̕����i�����j�����肷��
�@�@�@�I�j�S�Ă̗̈�̕����i�����j�����肷��
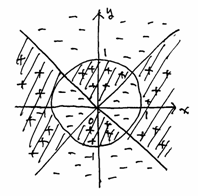 �@�u�s����
�@�u�s����![]() �̕\���̈��}������v
�̕\���̈��}������v
�@�i���j![]() �Ƃ����A���̈�����߂�B
�Ƃ����A���̈�����߂�B
�@�@�@�i��`��́A���W���ʑS�́j
�@�@�@�@���E���́A![]()
�@�@�@�@![]()
�@�@�@�i�����̋K���ɂ��j�ΐ��������߂�̈�ł���B