’05杜陵サークル3月例会の案内
厳しい冬も次第に勢いを失い、わずかな春の兆しが嬉しいこの頃です。学校も年度末を控え何かと慌ただしい時期ですが、サークル会員の皆様はお変わりなく元気でしょうか。さて、杜陵サークルの3月例会を次の日程でもちます。なお、例会終了後にいつもの月見亭で“桃の節句を祝う会”をもつ予定ですので、こちらの参加もよろしくお願いします。
記
1 日 時 3月5日(土)pm4:00から7:30まで
2 場 所 岩手大学教育学部小宮山研究室(407号)
tel 019-621-6539 fax 019-621-6543
3 サークル例会 実践レポート発表・検討、教具作り& 数学雑談
全国研究会議の報告
インフォメーション
○2月12日(土)、13日(日)広島市の鈴峯女子高と世羅別館で全国研究会議がもたれ、岩手から小宮山・下町・宮本・下河原・木下・伊藤の6名が参加しました。全体討論では、京都大の松下先生の「100マス計算をこえて−パフォーマンス・アセスメントの意味−」についての提案と東京の小寺先生の「習熟度学級の背景と問題点」についての報告。分科会「いま習熟の意味を問う」では下町先生が発表。“グノモン”を用いた数列の話でおおいに盛り上がりました。なんでも彼は“グノモン協会”を創立するという噂もあります。全国委員会では、2006年全国大会の骨子が承認されました。また一行は広島の食道楽を堪能。お好み焼き・かき料理など“食べる&飲む”のハードな行状で○先生などはかきの食い過ぎで腹をこわすありさまでした。
○雑誌「理系の数学」3月号に山下純一氏が「数学史を読む/高田の定理」(円に内接する五角形の各辺の両端と対角線の交点でできる5つの円の交点は同一円周上にある)を取り上げています。その中で、宮本先生の取れたて通信のことが詳しく紹介されています。実はこの雑誌を探したのですが、さわや書店では売り切れ、東山堂は扱っていないということでした。数学を取り巻く環境は着実に悪くなっているんだなーと感じました。ハイ!
○2月5日(土)岩大教育学部数学科の修士論文発表会で、金濱先生が「射影幾何」の発表を行いました。その日いつもの月見亭でサークル会員有志のささやかなご苦労さん会を持ちました。(単なる飲み会ではない!)この論文の別刷りはそのうち発刊とのことですので買って読みましょう。
○先月試作した“ネコ仙人Tシャツ”をジーとながめていた下町婦人が「このネコ仙人の仙衣は変じゃない!」と叫んだそうです。理由は、首のあわせが逆になっているというもの。これでは“死に装束”なのだそうです……ゲゲゲ……。
○絶好調の宮本先生と下町先生のホームページ。宮本先生のホームページの中に杜陵サークルのコーナーがあります。皆さんのぞいてみよう。
下町先生のHP http://www5b.biglobe.ne.jp/~simomac/
宮本先生のHP http://homepage1.nifty.com./toretate/
1月例会の様子
1月29日(土)の杜陵サークル12月例会の様子をお知らせします。
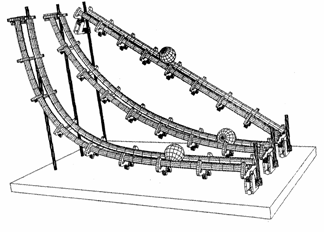
●最速降下線(サイクロイド)の実験 井上具規(花巻北高校)
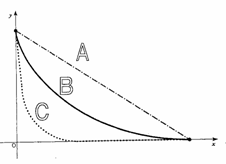
生徒に左のA,B,Cの坂のうち、上から球を転がして、一番早くしたに到着するのはどれかと質問したところ、Aは0名で、B、Cがほぼ同数であった。それぞれ、球を別々に転がして再度挙手させてみた。Aは明らかに遅いが、BとCはほぼ同時刻、人数は変わらず、Cの方が早いという生徒が多い感じであった。下のような実験器具(昔バンダイから出されていたスペースワープ)を使って、B:サイクロイド曲線が早いということを実感していた。
●デザイン定規でサイクロイド 下河原英(軽米高校)
内サイクロイドとその仲間の曲線を描くツール『デザイン定規』(レモン株式会社製)を100円ショップで見つけたので、たくさん買ってきました、皆でいろいろな曲線を描いて楽しみましょう。さて、この定規を使って外サイクロイドを描くにはどうしたらよいだろうか。
 また、サイクロイドを描くような定規はどうして作ったらようでしょうかね?
また、サイクロイドを描くような定規はどうして作ったらようでしょうかね?
●学問のすすめ・ぐのもんのすすめ 下町壽男(花巻北高校)
1 ぐのもんとは

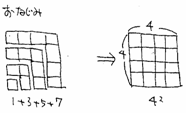 2 ぐのもんの技
2 ぐのもんの技
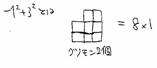
(1)奇数の和
つまり奇数の和は、平方数になる
![]()
(2)立方和
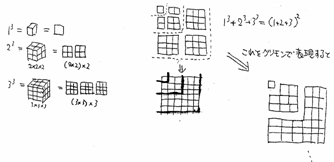 (3)群数列の部分和
(3)群数列の部分和
つまり、
![]()
(4)奇数の平方の交代和
![]() を考える。
を考える。
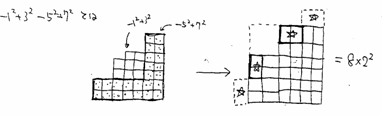
このことから、![]() がわかる。
がわかる。
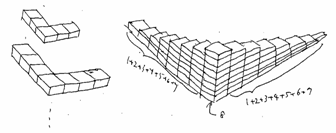 (5)自然数の和
(5)自然数の和
厚みのあるグノモンを作って見よう。
![]() より
より![]()
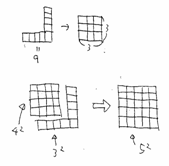 (6)ピタゴラス数
(6)ピタゴラス数
もし、グノモンが平方数だったらピタゴラス数が作れる。
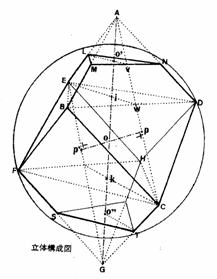
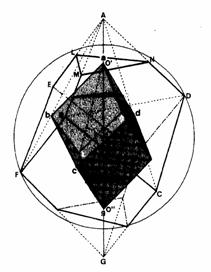
●デューラーの八面体 宮本次郎(釜石南高)
デューラーの版画「メランコリアⅠ」の中に登場する不思議な立体「デューラーの八面体」の模型を作ってみた。この立体が「接頭斜方六面体」であることは誰でもわかるが、その斜方六面体がどのような平行四辺形で囲まれたものか、どの位置で切り取ったものか諸説がある。ここでは、アーティスト榎本和子氏の解釈をとる。
ペンタグラムの中に現れる角が72°の平行四辺形(菱形)ABCDでできる斜方六面体を考える。この平行四辺形の1辺をAM:MB=AN:ND=φ:1となるような黄金比による分割点M,Nをとり、このMNで切り取ってできる五角形MBCDNを6枚あわせてできる八面体を考える。これを、デューラーの8面体と呼ぶことにする。
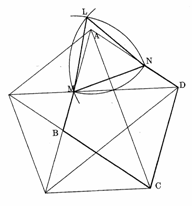
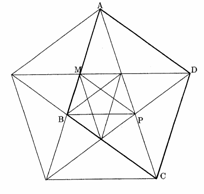
榎本氏によるとデューラーの八面体は、一つの球に内接すると主張している。本当か計算してみたらなんとピッタリ内接するではないか。また、この八面体には図のようにもととなる斜方六面体が内接し、自己相似形の無限の「入れ子」構造になっている。この比は黄金比であればかっこいいが、はたしてどうだろうか?
●準正多面体の体積と表面積 その1 下河原英(軽米高校)
準正多面体は13種類あるらしいが、まず簡単そうな立方八面体から取り扱ってみる。正六面体の8つの頂点から正三角錐各辺の中点まで切り取ると立方八面体ができる。
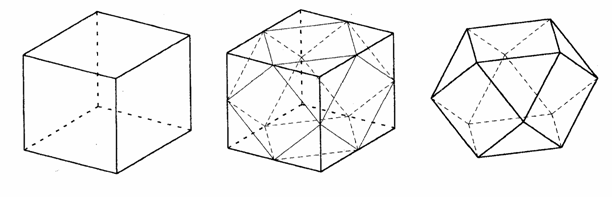
正三角錐を取り除く前の正六面体の1辺の長さをa,立方八面体の1辺の長さをb、体積をV、表面積をS、外接球の半径をR、内接球の半径をrとすると、次のようになる。
![]()
また内接球はないことがわかる。
●3つの円に外接する円を作図する方法 井上具規(花巻北高校)
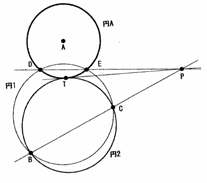 3つの円に外接する円を定規とコンパスだけで作図する方法を考えてみよう。準備として次の2つの作図法を考える。
3つの円に外接する円を定規とコンパスだけで作図する方法を考えてみよう。準備として次の2つの作図法を考える。
作図1)1つの円Aと2点B、Cが与えられているときの外接円
1 点B、Cを通り、円Aに2点D、Eで交わる円Iを作図する。
2 直線DEと直線BCの交点をPとする。
3 Pから円Aに接線を引き、その点をTとする。
4 3点B、T、Cを通る円2が求める円である。
作図2)2つの円A、Bと点Cが与えられているときの外接円
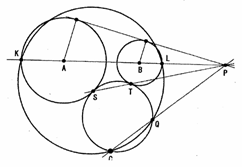 1 円A、Bの相似の中心Pを作図する
1 円A、Bの相似の中心Pを作図する
2 直線ABと円A,Bとの交点をK、Lとする。
3 3点C、K、Lを通る円と直線CPの交点をQとする。
4 円Aと2点C、Qで作図1を使って円を作成する。
これが求める円である。
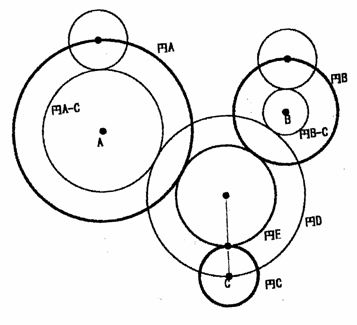
作図3)3つの円A、B、Cが与えられているときの外接円
1 円Cの半径の分だけを半径を減らした円A−C,B−Cを作図する。
2 2円A−C,B−Cと点Cにおいて作図2を使って円Dを作図する。
3 円Dを円Cの半径分だけ減らした円Eが求める円である。
●円錐曲線における極関係 金濱千明(盛岡第一高校)
非退化な円錐曲線を
![]()
考える。これは2次形式であることから行列を用いて
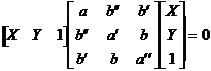
とも表される。さらに
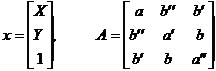
とおくと、
![]()
と表される。極形式 ![]() をつかうと次のようにも表される。
をつかうと次のようにも表される。
![]()
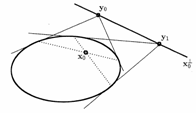
円錐曲線Cの方程式 ![]() とする。二点
とする。二点 ![]() に対して、
に対して、 ![]() をみたすとき、点
をみたすとき、点![]() と点
と点![]() は円錐曲線Cに関して共役であるといい、
は円錐曲線Cに関して共役であるといい、 ![]() と表す。また、点
と表す。また、点![]() を固定したときの直線
を固定したときの直線 ![]() を点
を点![]() の極線と呼び
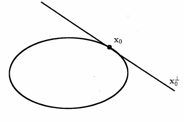
の極線と呼び![]() と表す。こうすると、点
と表す。こうすると、点![]() が円錐曲線C上にあれば、
が円錐曲線C上にあれば、
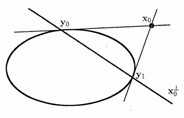
極線![]() は接線を表す。また、点
は接線を表す。また、点![]() が円錐曲線Cの外にあれば、極線
が円錐曲線Cの外にあれば、極線![]() は割線を表す。そして点
は割線を表す。そして点![]() が円錐曲線Cの中にあれば、極線
が円錐曲線Cの中にあれば、極線![]() は図のように極線C出会わない直線を表す。
は図のように極線C出会わない直線を表す。
●背理法の指導メモ 伊藤潤一(盛岡北高校)
新課程では数学Aに論理教材が配置されている。中味は「必要条件・十分条件」と「逆・裏・対偶」で、これは従来の数学Aにあった教材である。しかし、新課程で新しく入ったものに背理法がある。今までは補足や発展教材としてオプションの取り扱いだったものが一応キチンと指導することにになった。ところが、現状の中学の数学(高校の数学でさえ)では、したとしても証明法は証明の書き方(パターン)の指導に留まっており、生徒達は、証明の意義・意味を理解していないことが多い。このような状況では、背理法を指導するのは極めて難しいといわざるをえない。
一方、高校で身につけたい2大証明法は、
数学的帰納法と背理法
といえる。前者では、自然数にかかわる命題を、帰納・発見し証明の篩いにかけるという数学本来の「前向き」のサイクルを学ぶことができる。また、後者では、正面から攻めるのが大変な命題を背後から攻めるということを通じて、数学本来の「深遠さ」を学ぶことができる。
背理法は、指導するのには困難だが、学ぶ意義はかなり大きい教材といえる。用は、指導法の問題であるということか。
§1 排中律の成り立つ世界
§2 数学と矛盾
§3 背理法とは
§4 背理法いろいろ
バスケットボールでは
動くきっかけはフェイクから
というコーチング用語がある。つまり、右に動きたいときは、まず左にフェイクしてデフェンスを左にさそっておいて、右を抜き、左に動きたいときは右にフェイクしてから左を抜くというものである。つまり、動きたい方向の逆にフェイクするのがデフェンスをうまく抜くコツなのである。動くときには、無意識のうちにフェイクできるように練習しなければならない。
背理法もこれと同様である。
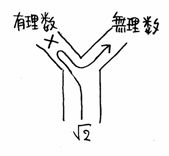
![]() は実数であるのは間違いないので、排中律により有理数であるか無理数のどちらかである。そこで、図のような、2またに分かれた道路を考える。
は実数であるのは間違いないので、排中律により有理数であるか無理数のどちらかである。そこで、図のような、2またに分かれた道路を考える。
無理数であることを証明したいのであれば、まず、反対側の有理数の方向に進む。あらぬ方向に進むと遅かれ早かれ、矛盾が発生するはずである。そうなったら大変なので、その方向に進むことは断念し、無理数の方向に進む他はない。
●杜陵サークルPresents 〜数学の小論文対策講座〜 下町壽男(花巻北高校)
東北大学理学部AO入試小論文問題B

【しもまっちの解答例】
![]() ・・・①
・・・①
を変形して
![]()
ここで、
![]()
![]() ・・・②
・・・②
とおくと
![]()
ここで、![]() とすれば、第二項→0となり
とすれば、第二項→0となり
![]() ・・・③
・・・③
①の焦点の座標は
![]()
である。
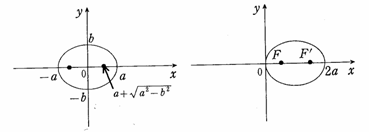
このとき、②の関係を使って
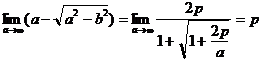
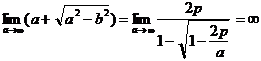
よって、![]() は放物線③の焦点
は放物線③の焦点![]() に近づき、
に近づき、![]() は無限遠点にとぶ。楕円は放物線に近づいていくことが、焦点の動きからわかる。
は無限遠点にとぶ。楕円は放物線に近づいていくことが、焦点の動きからわかる。
