’05杜陵サークル４月例会の案内

　

　春は花粉症とともにやってきました。心嬉しさと不快さを伴うこの季節は、期待と不安の新入生の心境とそっくりかも。さて、杜陵サークルの４月例会を次の日程でもちます。今回はなんと東京から増島先生がわざわざおいでくださるとのことですので、いつもよりパワーアップしたサークルになるのは必至でしょう。新年度第１回の例会でもあるので、新しい仲間も誘って参加したいものです。

　なお、例会終了後にいつもの月見亭で“新学期を祝う会”をもつ予定ですので、こちらの参加もよろしくお願いします。

 

記

 

１　日　     時　４月２日（土）ｐｍ４：００から７：３０頃まで

２　場　     所　岩手大学教育学部小宮山研究室（４０７号）

　　　　　    　 tel 019-621-6539  fax 019-621-6543

３　サークル例会  実践レポート発表・検討、

　　　　　　　　 教具作り& 数学実験、

　　　　　　　　 増島高敬先生の特別レポートなど

 

インフォメーション

● ３月は転任の季節でもあります。金濱先生は、県外交流で秋田県の大曲高校に転任することになりました。「比較的近いので、毎月のサークルには参加したい！」という力強いことばをもらいました。

● ５月１４日、１５日の東北民教研磐梯熱海集会そして６月２３日、２４日の東北地区合宿研究会（盛岡）の準備がはじまりつつあります。ＡＭＩ全国大会にむけて事務局の体制の確立と大会の運営（分科会・講座・講演）をつめなければなりません。いろいろな提案＆アイデアを寄せてください。

● 絶好調の宮本先生と下町先生のホームページ。宮本先生のホームページの中に杜陵サークルのコーナーがあります。皆さんのぞいてみよう。

　　　下町先生のHP　　http://www5b.biglobe.ne.jp/~simomac/

　　　　宮本先生のHP　　http://homepage1.nifty.com./toretate/

 

３月例会の様子

　３月５日（土）の杜陵サークル３月例会の様子をお知らせします。

●正１２面体を切り出す　　　　　　　　　　　　　　　　　　　宮本次郎（釜石南高校）

　２月１１日山口県防府市の山口宏さんの工房にいき、立方体の木材から多面体を切り出す作業を見学した。この作業工程に触発されて、生徒が教室で実際に工作できるような方法を考えた。

　正１２面体は、辺の比が１：φ^２の長方形を下の図のような位置に、３枚組み合わせて作ることができ、これより頂点Ａ，Ｂ，ＣとＡＢの中点Ｍの座標を図のように決めることができる。

　

 

　正１２面体の隣り合う２つの面のなす角θは、とのなす角として計算される。

したがって、立方体の一つの面と

という角度で、次の図のように切り取っていけばよいことがわかる。

　立方体の面と所定の角度をなす面で切り取れるような機械をつくる。簡単で安全な工作ができるようにするために、材料としては発泡スチロールを用いて、切断には電熱線による発泡スチロールカッターを使うことにした。切断面がなるために電熱線を固定して工作台を平行にスライドさせるようにする。切断場所の微調整ができるように、縦方向にスライドする工作台をのせる。さらに、切断する角度を調整するために発泡スチロールを固定する台を回転できるようにする。このようにしてできた工作機械を使って切断した結果、立方体から正１２面体を見事に掘り出すことができた。

 

●解の公式の歌スペシャル　　　　　　　　　　　　　　　　　　下町壽男（花巻北高校）

　ご存じ八戸の中村潤先生のオリジナル・ソング『解の公式の歌』を、ジャズギターの伴奏にのせてシモマック風でアレンジしたものの紹介、７つのバージョンが実におもしろい。そのうちＣＤになるかも？

　１　オリジナルバージョン（フォーク歌声系）

２人で歌った解の公式を歌う

　２　クラシックバージョン（バッハ「平均律クラヴィア」、グノー「アヴェマリア」風）

 

２人で歌ったの解の公式を歌う

　３　ボッサバージョン（wave remix）

平方完成で解を求める歌

　４　ジャズバージョン（misty remix）

グラフで解を求める歌

　５　演歌バージョン

解の公式のは思い出したが、√の部分は忘れてしまったときの解を求める歌

　６　シャンソンバージョン（autumn leaves remix）

解と係数の関係を使って解を求める歌

　７　ロック／ブルースバージョン

ＣＯＭＭＩＮＧ　ＳＯＯＮ！

 

●フレーム構造の正１２面体を平面につぶす　　　　　　　　　　井上具規（花巻北高校）　　　　　　　　　　　　　　　

　フレーム構造の正六面体は、面が正方形であるため平行にスライドしながら平面につぶすことができる。では、正１２面体はどうだろうか？実は、平行にスライドするだけではつぶすことは出来ない。一番上の正５角形をひねることで平面までつぶすことができる。図のように全ての辺の長さが同じであること、一番外側が正１０角形であること、正五角形の隣は60°であることなどが特徴である。

 

●こまを作ろう　　　　　　　　　　　　　　　　　　　　　　　井上具規（花巻北高校）　

　半径ａの円柱を左のように45°の角度で切った図形の重心を求め、この重心を通るコマの軸を考えコマを作成しよう。

　重心の求め方として、次の４通りの方法を考え、

∫位置・重さ／∫重さ

によって計算する。分母は３次元の場合体積になることに注意しよう。

（１）ｘ軸に平行に切る

　切断面の重心の位置は、体積はであるので、重心の位置は

　同様にして（２）ｙ軸に平行に切る（３）放射状に切る

（４）バウムクーヘン状に切るとしても求めることができる。

　実際、心棒が重心を通るコマを３タイプ木工で作成してみたのだが、うまく回ったのは一番右側だけであった。重心を通っていてもコマにはならないことがあるのだなぁ。

　安定してまわるコマを作るには、図のように重心Ｇを通り軸に垂直に上下に分けたときに得られるそれぞれの重心Ｓ、Ｔが軸の上にあればよいようである。この条件に合うコマを２つ作り実験したら。右のコマはよく回ったが左のコマは安定こそすれ長くは回らない。まだまだ考える余地がありそうである。（立体の重心と空間の回転は、平面のそれよりかなり複雑らしい）

 

 

●デューラーの八面体（つづき）　　　　　　　　　　　　　　　　宮本次郎（釜石南高校）

　デューラーの八面体とは、角の一つが72°の菱形ＡＢＣＤの６枚で作られる斜方六面体（平行六面体）の向かい合った２つの頂点を図のように

（黄金比）

に切り取った接頭斜方六面体のことである。前回のレポートでは、この立体は球に内接することを示した。

　このオブジェを作成した榎本和子氏によれば、この立体に相似な斜方六面体が内接していてその相似比が黄金比になっていると説明している。つまり、この立体はその比が黄金比の自己相似形の無限「入れ子」構造をもっているという極めて魅力的な主張である。しかし、残念ながらこの比が黄金比では自己相似形にはならないことが示すことができた。

　さらに、自己相似形を維持するような比は

（黄金比の近似）

であることが示せる。このときは綺麗に自己相似形の「入れ子」ができる。しかし、惜しいことにこの比で作ったデューラーの八面体（もどき）は球に内接しなのである。

 

 

●杜陵サークルPresents〜数学の小論文対策講座〜　　　　　　　　下町壽男（花巻北高校）

　次の問題は、2001年の宮城大学の問題である。　

 

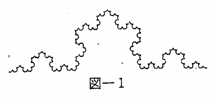『次の説明を読んで、問１から問３に答えなさい。図１はコッホ曲線と呼ばれる曲線である。

コッホ曲線は、以下の手順により作成される。

�@長さ１の曲線を描く

�Aこの線分を３等分する

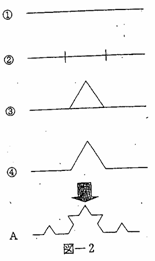�B３等分した線分の中央の線分を底辺とした正三角形を描く

�C３等分した線分の中央の線分を消去する

�D各線分に対して�Aから�Cの手順を繰り返す

　図２の�Cをひとつの図形単位とすれば、Ａは�Cの図形を相似比に縮小した４個の図形から構成されていりことになる。このように図形全体が、その図形を相似比に縮小したミニチュア個により構成されている図形をフラクタル図形、このときのｄの値をフラクタル次元という。コッホ曲線の場合には、である。

問１　コッホ曲線のフラクタル次元ｄの値を小数第２位まで求めなさい。ただし、とする。

問２　図３は正三角形を基本図形としたフラクタル図形であり、シルピンスキーのガスケットと呼ばれる。図３を作成するできるだけ少ない手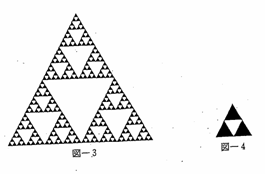順を示しなさい。

問３　図４に示す三角形をひとつにの図形単位としたとき、図３のフラクタル次元を小数

第２位まで求めなさい。』

 

Ｓ：いまいち書いてあることがわかりません。

Ｔ：普通「次元」という言葉にえがくイメージとはどんなものですか？

Ｓ：１次元は直線、２次元は平面、３次元は空間というイメージです。

Ｔ：この問題では、次元を「縮小」と「貼り付け（被覆）」によって表現しています。キーワードは「自己相似性」です。では、今あなたがイメージした次元を例にとってみましょう。まず、１次元の代表として、下図のような線分ＡＢを考えましょう。

これをに縮小すると、

このに縮小した線分を２つ集めてつなげると、もとの線分が再生されますね。次に、平面の代表として、図のような正方形を考えてみましょう。

これも縮小コピー機を使って、図のようにに縮小します。これは、４つ集まると元の正方形が復元されることがわかります。最後に３次元の例として立方体を考えてみましょう。

これは、に縮小したものを８個集めると自己再生されることがわかります。ここまでの話をまとめると、

　�@１次元　に縮小したものを２つ集めると自己再生

　�A２次元　に縮小したものを４つ集めると自己再生

　�B３次元　に縮小したものを８つ集めると自己再生

これらを

�@　　　�A　　�B

とすると、ちょうど指数のところが次元を表す数に対応しています。

Ｓ：なるほど、わかりました。つまり、

「にしたものを８つ集めると自己再生される」図形は、「」より３次元です。よって「にしたものを４つ集めると自己再生される」図形は、「」より次元は、ですね。

【解答】

      より、次元Ｄは、≒1.26

Ｔ：そうです。この問題で定義されている「フラクタル次元」の説明はちょっとわかりにくいかもしれませんが、このように図形の自己相似性に着目すると、結構自然な定義になります。このような次元を「相似性次元」といいます。

（中略）

Ｓ：次元が整数にならないということはどういう意味を持つのでしょうか。

Ｔ：つまり、１次元より上で２次元より下という面をもつ図形です。

例えば、コッホ曲線の線分の長さを計算して見ましょう。

　第１世代の線分を１とすると、

　第２世代は、

　第３世代は、

　第４世代は、

となります。つまり、第ｎ世代はであるので、とすると、線分の長さが∞に発散していることがわかります。このようなことから、コッホ曲線は１次元でありながら２次元の様相を持っている図形とみることができます。

（後略）

 

●魔方陣の平方回文性質　　　　　　　　　　　　　　　佐々木義卓（岩手大学大学院生）

　次の魔方陣の注目すべき特殊な性質をよく見よ。

（行）

（列）

（対角）

（反対角）

（対角）

（反対角）

この性質はDr.Irving Joshua Matrixによって発見された。このレポートはすべての３行３列魔方陣はこの性質を満足することを証明している。ここで、行、列、対角、そして反対角は任意の基底をもつ３桁の数として読まれる。この性質を

平方回文的性質（square-palindromic property）

と呼ばれるらしい。魔方陣がこのような平方回文的な性質を持っているとは驚きである。おもしろい！

だだし、証明は省略する。詳しくは、Mathematical Monthly, 166(1999)を見てほしい。

 

●整方程式の存在範囲　　　　　　　　　　　　　　　　　　　　伊藤潤一（盛岡北高校）

　ガウスの代数学の基本定理によれば整方程式は複素数の範囲で必ず解をもつことになる。しかし、この定理は“存在定理”であり、解が実際にどこにあるかは示してくれない。その解は一体どこにあるだろうか？

一般の整方程式を考える前に、とりあえず３次方程式を考えよう。

　実係数の３次方程式

の解をα、β、γとする。この解の重心を

と定義すると、解と係数の関係から

となる。３つの解はこの重心を中心として存在することになる。

そこで、平行移動によって、解の重心が原点になるようにすると、当然ではあるが２次の項が０になる。このような変形をして３次方程式を解いたカルダノにちなんで最高次の項の次の項を消す変換は

カルダノ変換

と呼ばれることがある。

　解は方程式の重心を中心に配置されるはずだから、これからは、このカルダノ変換を施した方程式を取り扱えば十分である。問題は、重心この場合は原点を中心としてどれだけの半径の円内に解があるかである。この半径を解の半径と呼ぼう。

３次方程式の解の存在範囲について次のことを示そう。

 

 

 

 

 

 

�Aの方程式の正の解は、ニュートン法や区間縮小法で近似解を求めればよい。では証明してみよう。

　　

とおく。ただしとする。方程式が正の解を持つことは　

より簡単にわかる。次に、より、

この方程式が２つの正の解を持つとすると、

辺々引いて整理するとが導け、唯一の正の解をもつことがわかる。

　さて、の解をとし、の正の解をとするとき、

  を示そう。

これより

　　

よって、

　すなわち　

は方程式の唯一の正の実数解だからとなる。これで証明できた。

同様にして次の定理がなりたつ。証明は３次の場合とほぼ同様である。

 

 

 

 

 

 

　

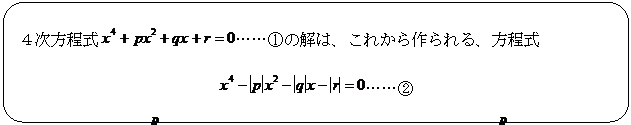
　最後に例題をやってみよう。４次方程式の解をとする。

さて、次の４次方程式

の正の解は

　　

より３より小さいことがわかる。よって、              すなわち、解は複素平面で原点を中心とした半径３の円内にある。（かなり大雑把だが、一応解の存在範囲が示せる）

　　

●理系への数学５月号について　　　　　　　　　　　　　　　　宮本次郎（釜石南高校）

　2005年５月号の理系への数学に「数学史を読む『高田の定理』山下純一」のコピーを提供してもらった。やはりこの定理はエポックメイキングだったんですねえー！皆さん読んでみてください。

 

●京都大学入試問題英語�Tについて　　　　　　　　　　　　　　宮本次郎（釜石南高校）

  2005年の京都大学入試問題英語�Tはなんと、有名な確率実験ビッフォンの針他の数学を取り扱っているそうです。原文を見ながら、数学をちゃんとやっている者はきっとうまく訳せたのではという感をもちました。