�@�f05�m�˃T�[�N���U�����̈ē�
�@���Ă̑��z���܂Ԃ����������̍��A�m�˃T�[�N���̉���̊F�l�����C�ł��傤���B���N�x�͂��߂Ă̊����l�����}���A�����ɂ�������ł���̂ł͂Ȃ��ł��傤���B���āA�m�˃T�[�N���̂U���������̓����ł����܂��B����́A�ʎ��̂悤�ɂ`�l�h�̓��k�n�捇�h������ɍ������Ă����ƂɂȂ�܂��B�܂��A���̉�́A�����g���w���番�ȉ�̊w�K������˂Ă��܂��B����́A�����̉��X�搶�̍u�����ڋʂł��傤�B�Z�������ł����A�V�������Ԃ�U���ĎQ������悤��낵�����肢���܂��B
�L
�P�@���@ ���@�U���Q�T���i�y�j�����P�F�O�O〜�Q�U���i���j�P�Q�F�O�O���܂�
�Q�@��@ ���@����w����w���@�Q�T���i�y�j�����P�F�O�O〜�T�F�O�O
�@�@�@�@�@�@�@�@ ���ۉ�ف@�Q�T���i�y�j�����V�F�O�O〜�Q�U���i���j�P�Q�F�O�O
�R�@���@�@�@ �e �u���u�Z���E���w�̎��ƂŐ������郏�[�h�E�G�N�Z���̗��Z�v
�@�@�@�@�@�@�@�@�@�i�u�t�@���X�@�m�搶�@�����n��`�l�h����E�_�ސ��w�j
�@�@�@�@�@�@�@�@ ���k�e���̏��E���E���̎��H���|�[�g���\�E����
�@�@�@�@�@�@�@�@ �Q�O�O�U�N�`�l�h�S�����i�Ԋ��j�̑ł����킹��
�C���t�H���[�V����
�� �U���P�P���i�y�j����w�Ŋ��`�l�h�̊g�厖���lj�c��������A��P�N�Q������ɔ������Ԋ����̏����ɂ��Ęb�������܂����B���̒��Łu���N�̂W���Q�V���i�y�j�ɏ��E���E���̑S�������̎��H�҂��Ăŋƍu���������A���̋@��Ɋ��̂`�l�h����𑝂₷�ƂƂ��ɉ���̃��x���A�b�v��}�낤�v�Ȃǂ��b�������܂����B
�� ���N�̑g�������́A���N�̑S�����̐�`�������ŋɂ߂đ�ɂȂ�Ǝv���܂��B�����ŁA�X��〜�P�O���̎x�������܂łɁu���O���ē��v�̃`���V�����邱�Ƃɂ��܂����B���́u�`���V�v�{�u�l�R��l�s�V���c�v�ő����`���A��������̐l�Ɏ��s�ψ��Ƃ��ċ��͂����肢����悤�ɂ��������̂ł��B
�� �W���R��〜�T���̂`�l�h�S���������L���W��̈ē����߂��͂��܂������H�L���͂��Ȃ�̉��u�n�ł����A����̑��̏����Ƃ������Ƃ�����F�ŎQ���ł�����悢�Ȃƍl���Ă��܂��B����ǂ̍��h���E�T�[�N���őł����킹���������ƍl���Ă��܂��B
�� ��D���̋{�{�搶�Ɖ����搶�̃z�[���y�[�W�B�{�{�搶�̃z�[���y�[�W�̒��ɓm�˃T�[�N���̃R�[�i�[������܂��B�F����̂����Ă݂悤�B
�@�@�@�����搶��HP�@�@http://www5b.biglobe.ne.jp/~simomac/
�@�@�@�@�{�{�搶��HP�@�@http://homepage1.nifty.com./toretate/
�T�����̗l�q
 |
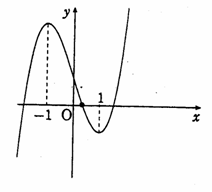
�@�O�p���̍����̎d���͋��ȏ��Ɏ��̂Q�ʂ肪��������Ă���B
�i�@�j���@�藝�̋t�œ������@
![]()
���̕��@�́A���̂Q�Ŋ������̂��̐������ꂵ���B
�i�A�j�⏕�}�œ������@
�@�⏕�}���A![]() ������@
������@![]()
 ���̕��@�́A��C�ɂł邪�C���������B�����ŁA����̎��Ƃł͎��̂悤�ɂ���Ă݂��B
���̕��@�́A��C�ɂł邪�C���������B�����ŁA����̎��Ƃł͎��̂悤�ɂ���Ă݂��B
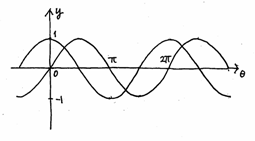
���O���t�ōl����
�@�����������T�C���J�[�u�̏d�ˍ��킹�����̂͂܂��A�T�C���J�[�u�ɂȂ邱�Ƃ��A�O���t�̗v���A�v���̓_���v���b�g���Ċm���߂�B
�@![]()
���̂悤�ȃA�i���O�I�ȍ�Ƃ́A���k�͏��߂Ă̌o���ł������悤�ŁA�͂��߂͂ǂ����Ă悢���˘f���Ă����B�����ŁA�R�c��`���B
�E �O���t�̕Е��̒l���O�̂Ƃ��́A�O�łȂ����̃O���t�̓_���v���b�g
�@�E�Q�̃O���t���d�Ȃ��Ă���Ƃ���ł́A�Q�{�ɂ����_���v���b�g
�@�E�O���t�̐��̕����ƕ��̕��������E���ĂO�ƂȂ�Ƃ����T���ăv���b�g
�E �ő�A�ŏ��ɂȂ肻���ȂƂ���������āA�v���b�g�����_���Ȃ����Ċ��炩�ȃO���t��`���B
�@�O���t������������A��������A�P�̃T�C���J�[�u�ɂȂ肻�����Ƃ����\�z�����Ă�B�܂�A
![]()
�ɂ܂Ƃ߂�ꂻ�����Ƃ����Ƃ��m�F����킯�ł��B
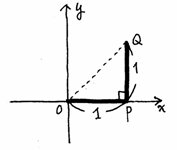 �����p�ɋȂ������܂���̉�]
�����p�ɋȂ������܂���̉�]
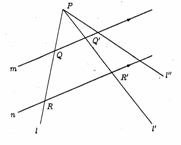
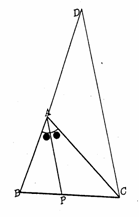
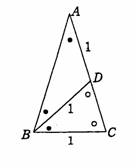
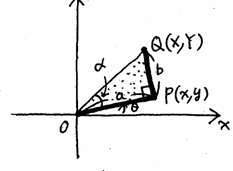
�@�}�̂悤�Ȑ܂���n�o�p���n�����_�A�n�o�������̐��̕����ɁA�p����P�ی��ɂ�����Ă���B���A���̐܂�����_�n�𒆐S�ɃƂ�����]�����Ƃ���B���̂Ƃ��̓_�o�̂����W��![]() �A�_�p�̂����W��
�A�_�p�̂����W��![]() �Ƃ���ƁA�}���
�Ƃ���ƁA�}���
![]()
![]()
�ƂȂ邱�Ƃ��킩��B�Ƃ������Ƃ́A
![]()
�̐U�镑���ׂ邽�߂ɂ́A�_�p�̓�����T��悢�B
�@�}��薾�炩�ȂƂ���A�_�p�͂n�𒆐S�Ƃ��ĉ�]�^��������B
�@���p�O�p�`�n�o�p�Ƀs�^�S���X�̒藝���g��
![]()
�ƂȂ�̂ŁA���̉�]�^���̓��a�̒�����![]() �ł���B�܂��A���a�n�p�͓��a�n�o���
�ł���B�܂��A���a�n�p�͓��a�n�o���
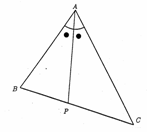
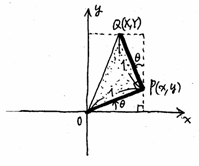
�@��ʂɁA�}�̂悤�Ȑ܂���n�o�p���n�����_�A�n�o�������̐��̕����ɁA�p����P�ی��ɂ�����Ă���B���A���̐܂�����_�n�𒆐S�ɃƂ�����]�����Ƃ���B���̂Ƃ��̓_�o�̂����W��![]() �A�_�p�̂����W��
�A�_�p�̂����W��![]() �Ƃ���ƁA�}���
�Ƃ���ƁA�}���
![]() �@�@�@
�@�@�@![]()
�ƂȂ邱�Ƃ��킩��B�Ƃ������Ƃ́A
![]()
�̐U�镑���ׂ邽�߂ɂ́A�_�p�̓�����T��悢�B
�@�}��薾�炩�ȂƂ���A�_�p�͂n�𒆐S�Ƃ��ĉ�]�^��������B
�@���p�O�p�`�n�o�p�Ƀs�^�S���X�̒藝���g��![]()
���A���̉�]�^���̓��a�̒�����![]() �ł���B�܂��A���a�n�p�͓��a�n�o���ڂo�n�p����
�ł���B�܂��A���a�n�p�͓��a�n�o���ڂo�n�p����
��������s���Ă���̂ŁA�_�p�̂����W�x��
![]()
�Ə������Ƃ��ł���B�������A![]()
���Ȃ킿�A
![]()
�ƂȂ�B���ǁA�O�p���̍����́A���p�O�p�`�n�o�p�̎ΕӂƁڂo�n�p�ׂ邱�ƂɋA�����邱�Ƃ��킩��B����ŁA�⏕�}�̈Ӗ����X�g�����D�ɗ������B
�������������T�C���J�[�u�̍���
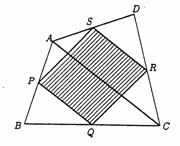
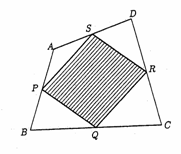
�@���������̃T�C���ƃR�T�C���������������̂̓T�C���J�[�u��`�����Ƃ��킩�����B
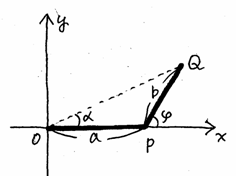 �@��ʂɁA�����������T�C���J�[�u�̏d�ˍ��킹�����̂͂܂��A�T�C���J�[�u�ɂȂ邱�Ƃ��ؖ����悤�B�܂�A
�@��ʂɁA�����������T�C���J�[�u�̏d�ˍ��킹�����̂͂܂��A�T�C���J�[�u�ɂȂ邱�Ƃ��ؖ����悤�B�܂�A
![]()
![]()
�ƕό`�ł��邱�Ƃ������B
�@���̂��߁A�}�̂悤�Ȑ܂���n�o�p���n�����_�A�n�o�������̐��̕����ɁA�p����P�ی��ɂ�����Ă���B���A���̐܂�����_�n�𒆐S�ɃƂ�����]�����Ƃ���B���̂Ƃ��̓_�o�̂����W��![]() �A�_�p�̂����W��
�A�_�p�̂����W��![]() �Ƃ���ƁA�}���
�Ƃ���ƁA�}���
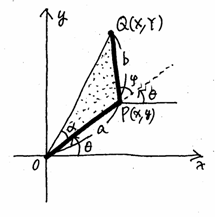
![]()
![]()
�ƂȂ邱�Ƃ��킩��B�Ƃ������Ƃ́A
![]()
�̐U�镑���ׂ邽�߂ɂ́A�_�p�̓�����T��悢�B
�}��薾�炩�ȂƂ���A�_�p�͂n�𒆐S�Ƃ��ĉ�]�^��������B
�@�O�p�`�n�o�p�ɗ]���藝���g��
![]()
���A���̉�]�^���̓��a�̒����ɂ�����B�܂��A���a�n�p�͓��a�n�o���ڂo�n�p������������s���Ă���̂œ_�p�̂����W�x��
![]()
�Ə������Ƃ��ł���B�������A
![]()
���Ȃ킿�A
![]() �ƂȂ�B���ǁA�O�p���̍����́A�O�p�`�n�o�p�̕ӂn�p�Ɓڂo�n�p�ׂ邱�ƂɋA�����邱�Ƃ��킩��B�������āA����������
�ƂȂ�B���ǁA�O�p���̍����́A�O�p�`�n�o�p�̕ӂn�p�Ɓڂo�n�p�ׂ邱�ƂɋA�����邱�Ƃ��킩��B�������āA����������
�T�C���J�[�u�{�T�C���J�[�u���T�C���J�[�u
���ؖ��ł����B