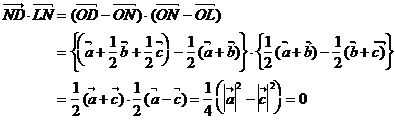杜陵サークル10月例会報告

　’05杜陵サークル１２月例会の案内

　秋冷の候、杜陵サークルの会員の皆様いかがお過ごしでしょうか？学芸の秋ですからきっと夜長を数学三昧で楽しんでいるでしょう。「それどころではない！」という声も聞こえてきそうですが、数学も人生も楽しまなくちゃね。さて、杜陵サークルの１０月例会を次の日程でもちます。忙しい中ですが、新しい仲間を誘って参加するようよろしくお願いします。また、サークル終了後いつもの月見亭で“中秋をめでる会”をもつ予定ですので、よろしくお願いします。

記

１　日　時　１２月１０日（土）ｐｍ４：００〜７：３０

２　場　所　岩手大学教育学部　小宮山研究室４０７号）

　　　　　　 tel 019-621-6539 fax 019-621-6543

３　内　　　容実践レポート発表・検討、

　　　　　　　　 教具作り& 数学実験

インフォメーション

● １１月１８日（土）、１９日（日）岩手高教組の教科別教研が花巻温泉千秋閣でもたれました。数学教育分科会は、小宮山先生の助言者をはじめサークルから下町先生の「別解コレクション」、宮本先生の「三角比の授業」、井上先生の「位相的多面体」、それに葛西先生から「数学通信」が発表し分科会を盛り上げました。また、推進委員長の下河原先生の運営と人徳により、たくさんの“若い先生”の参加も得て活発な議論がなされました。

● １１月２３日（水）ＡＭＩ全国大会に向けての岩手県の第１回準備委員会が岩手大でもたれ、地元岩手としてどう準備をすすめるかの話し合いをいたしました。今回の会議では、必要な仕事と人員の確認を中心に話し合いました。まだまだ多くの人員が必要であることが確認されました。今後多くの人に呼びかけていきたいものです。

● １１月２６日（土）、２７日（日）青森市の青森教育会館でＡＭＩ東北地区研究大会がもたれました。後援は、中央の研究局長の足立久美子先生の教師の生き様を熱く語る講演や宮本先生の「マンガで三角比〜イズミとジローの数学物語」の講座、小倉先生の「図形の指導〜二等辺三角形の内心・外心・重心・垂心」、鳩岡先生の「考えさせる授業〜平方完成〜」、伊藤先生の「オイラー線とオイラー円」のレポートなどとても好評でした。また、２７日（日）の昼からはＡＭＩ花巻大会の第３回実行委員会がもたれ、大会予算等の話し合いがなされました。

● “家庭の算数・数学百科”（日本評論社）の売れ行きは、とてもわかりやすく「寝ころびながらでも読める辞典」ということでとても好調のようです。サークルの６名も著者に入っていますので、たのめば“八掛け”で手に入るはずです。個人でまた学校の図書館に普及したいものですね。

● 冬の民教研は１月１４日（土）、１５日（日）に宮古市でもたれます。案内が届いているでしょうか？例年と日程が異なっているので注意してください。

● 絶好調の宮本先生と下町先生のホームページ。宮本先生のホームページの中に杜陵サークルのコーナーがあります。皆さんのぞいてみよう。

　　　下町先生のHP　　http://www5b.biglobe.ne.jp/~simomac/

　　　　宮本先生のHP　　http://homepage1.nifty.com./toretate/

１０月例会の様子

１０月２９日（土）杜陵サークル１０月例会の様子をお知らせします。

●スライド積分　　　　　　　　　　　　　　　　　　　　　　井上具規（花巻北高校）　

　アステロイドの面積は、

と計算できる。ところが、極座標の面積公式で計算しよう。に注意して変形すると、

となって、前の計算結果と違う！なぜこうなったのだろうか。

　間違った原因は、極座標で表された曲線において、として

すなわち、曲線

の面積を計算していたのである。

　それでも、強引に極座標に直す。

２項目において、とすれば

となるから、と考えて計算することができる。すなわち、

実際には、としたとき、

を考えて、曲線上をスライドさせながら面積を計算することができる。

●数遊び　　　　　　　　　　　　　　　　　　　　　　　　　佐々木義卓（岩手大院生）

　先日、岩手大の川田先生から次のような問題が提示された。（お遊びで！）

『○に１〜９９の相違なる数をいれ、（□の最大数）−（□の最小数）が最小の人が勝ち。』というゲームで、このゲームでは（□の最大数）＝（□の最小数）ならば無敵である。では、そのような□が見つけられるかという問題である。川田先生によれば、□が全て同じになるように○を埋めることもできるし、□が連続した数になるように○を埋めることもできるとのこと。

　各○、□にそれぞれを代入する。すなわち、

上記は次のように書ける。

　川田先生から出題された問題は、およびとして考えるわけである。ここで問題を簡単にするために、条件を弱くして考えることにする。まず、各は任意の整数でもよいものとする。さらに、およびはそれぞれ互いに素とする。

　かつとすれば、次のような結果を得る。

●ウルトラスーパーハイレベル講座３〜１／ｆに迫る〜　　　　　下町壽男（花巻北高校）

Ｔ：今日は１／ｆゆらぎについて私の知る範囲で、簡単な説明を行いたいと思います。

Ｓ：まず、「ゆらぎ」とは何なのですか？

Ｔ：そうですね。まず、そのことから説明しましょう。「ゆらぎ」の第１人者である、武者利光先生（東工大）の言葉によると『ものの予測のできない空間的、時間的変化』ということだそうです。

Ｓ：それって、でたらめな運動ということですか。

Ｔ：いや、「でたらめ」ではないのです。「でたらめ」と「規則性」の間の状態という感じですね。

（中略）

Ｓ：つまり、ゆらぎとは、

「規則性」と「意外性」が拮抗した状態といっていいのですね。

何か具体的なものを示してください。

Ｔ：一番よく例に出されるのは、そよ風ですね。そよ風は一定の強さではなく、強くなったり弱くなったりゆらいでいます。それから、小川のせせらぎとか、音楽も時間と共に音の高低や大小が変化しているので、ゆらぎと見ることもできます。人間の心拍数や体温の変化もゆらぎの一つですね。

Ｓ：では、１／ｆのゆらぎとはなんでしょうか。

（中略）

Ｔ：ええと。では、バスケットボールの話をしたいと思います。今、Ａ君が、バスケットのフリースローを何度も行ったとします。入ったときを○、はずしたときを×とすると、時間と共に変化する１つの系列をつくることができますね。例えば結果が、

という結果だったとします。

これらのゆらぎを調べてみます。まず、周期を無理やり導入してみましょう。○○○・・・とずっと○が続くのを周期１とします。また、○×○×・・・と１回おきに○が起こるものを周期２とします。次に、○××○・・・と２回おきに○が起こるものを周期３としましょう。このように周期を定義すると、上の結果から、各周期ごとにその回数はどうなるのでしょう。

Ｓ：つまり、周期１は、○○という状態が何回起きているか調べればよいのですね。

下の表のようになりました。

Ｔ：ここで、周期ｓと出現回数Ｐをグラフに表すとどのようになりますか。

Ｓ：図のようになります。

Ｔ：先ほどあなたが行った表が、いわゆる周波数ごとの波の強さをスペクトル分解して分析したということになります。そして、スペクトルの強さはここでは、「出現回数」ということになるのです。

Ｓ：なるほど。そして、そのグラフを見ると、シュートをした人の特性がわかるのですね。

Ｔ：周波数にあたる１／ｓとスペクトルの強さにあたるＰが比例しているとき１／ｆゆらぎというのです。

●オイラー円とオイラー線　　　　　　　　　　　　　　　　　　伊藤潤一（盛岡北高校）

　４年ぶりにベクトルの授業をした。今までは、半ば自明な図形の性質を調べるのに、わざわざベクトルという“仰々しい武器”を使うことに何となく違和感があった。なにもベクトルを使わなくても、「初等幾何的アプローチ」または「解析幾何的アプローチ」でいいのではないかという思いがあったのである。

　今回のレポートは、ベクトルという“武器”を存分に生かした教材をどう開発・組み立てていけばよいかという思いから書いたものである。三角形のオイラー線とオイラー円（九点円）そしてその拡張としての円に内接する四角形のオイラー線とオイラー円の性質をベクトルで調べてみることにする。

　高校生にとってすこし難しいかもしれないが、興味をもって取り組めるコンテンツではないだろうか？

　△ＡＢＣの頂点Ａ，Ｂ，Ｃから対辺に下ろした垂線の足をそれぞれＰ、Ｑ、Ｒとし、ＡＰ，ＢＱ，ＣＲの交点をＨとする。この垂心Ｈの位置ベクトルを求めよう。

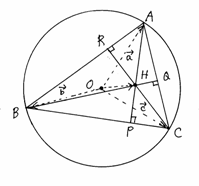　△ＡＢＣの外心をＯとしてとすると、

・・・①

が成り立つ。証明は次のようにする。

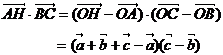
これより、がいえる。同様にして、より、より

から、点Ｈは垂心であることがわかる。

　△ＡＢＣの重心Ｇの位置ベクトルは、であるので、がいえて、３点Ｏ，Ｇ，Ｈが一直線上にあり、しかも、であることがわかる。この直線は、オイラー線と呼ばれている。

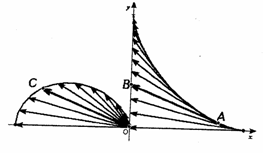
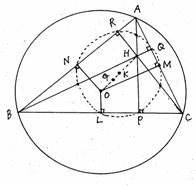　次に、線分ＯＨの中点をＫとすると、この点Ｋの位置ベクトルは、となる。また、垂線ＡＨ，ＢＨ，ＣＨの中点をそれぞれＤ，Ｅ，Ｆとすると、これらの点の位置ベクトルは、

となる。

　△ＤＬＰに注目しよう。∠ＡＰＬ＝９０°より、点Ｐは直径がＤＬの円周Ｃ上にあることわかる。さらに、△ＡＢＣの辺ＢＣ，ＣＡ，ＡＢの中点をそれぞれＬ，Ｍ，Ｎとする。このとき、

より。つまり、∠ＤＮＬ＝９０°であるので、点Ｎも、直径がＤＬの円周Ｃ上にあることわかる。同様にして、点Ｍも、直径がＤＬの円周Ｃ上にあることわかる。また、

よりつまり、∠ＤＥＬ＝９０°であるので、点Ｅも、直径がＤＬの円周Ｃ上にあることわかる。同様にして、点Ｆも、直径がＤＬの円周Ｃ上にあることわかる。このようにして、９点Ｄ，Ｅ，Ｆ，Ｌ，Ｍ，ＮとＰ、Ｑ、Ｒが同一円周Ｃ上にがあることがわかる。

　また、線分ＬＤの中点は、

である。これはに等しいので、点Ｋは、この円Ｃの中心であることがわかる。したがって、三角形ＡＢＣの３つの中点、３つの垂線の足、３つの頂点と垂心の中点を通る円が存在することがわかる。この円は、オイラー円または九点円と呼ばれる。オイラー円の中心はオイラー線の中点で、半径は三角形の外接円の半分であることがわかる。