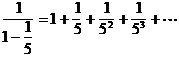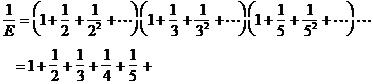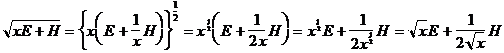�@�f06�m�˃T�[�N���Q�����̈ē�
�@�����܂��Ă��߂łƂ��������܂��B�m�˃T�[�N���̉���̊F�l�����ɂ��������撣���Ă��܂����H�R�N���S���̐搶�͂��悢��d�グ�̎����ɓ���A���g�݂����M���Ă��邱�Ƃł��傤�B���āA�m�˃T�[�N���̂Q���������̓����ł����܂��B����̃T�[�N���́A�����Q�F�O�O����s����S�����̏�����̂��ƈ�������������܂��B�܂��A����́A�����̉��X���i�_�ސ��j���Q������\��ł��B�Z�������ł����A�V�������Ԃ�U���ĎQ������悤��낵�����肢���܂��B�܂��A�T�[�N���I���ア���̌������Łg���t���j����h�����\��ł��̂ŁA��낵�����肢���܂��B
�L
�P�@���@ ���@�Q���S���i�y�j�����S�F�R�O〜�V�F�R�O
�Q�@��@ ���@����w����w���@���{�R�������S�O�V���j
�@�@�@�@�@ �@ tel 019-621-6539
fax 019-621-6543
�R�@���@�@�@ �e ���H���|�[�g���\�E�����A
�@�@�@�@�@�@�@�@ ������& ���w����
�C���t�H���[�V����
�� �Q���S���i�y�j�Q�F�O�O〜�S�F�O�O����w����w���ł`�l�h�S�����̏����ψ��������܂��B�T�[�N������̊F�l�͂ł��邾���s�������Ă�����̕����Q�����Ă��������B���̎��s�ψ���ɂ͒������牽�X�搶�A���k�n�拦�̈ψ����̒����搶���Q�����邱�ƂɂȂ��Ă��܂��B
�� ���N�̖������́A�P���P�S���i�y�j�P�T���i���j��
�� �P���P�T���i���j�ɓ������E���������̐V�t�u���������̐_�y��ł�����A�ɓ��搶���u���w������y���ށv�Ƃ����e�[�}�ōu�����܂����B�w�`�u�h�d�q�V���[�Y�̋���D�]�������Ƃ̂��Ƃł��B
�� �P���P�R���i���j��������Z���^�[�̌������\��ʼn��͌��搶���u�����A�g�̐��w�Ȃ̎��g�݂ɂ��āv�̃��|�[�g���\�����܂����B�ƂĂ��D�]�������悤�ł��B
�� �Q���P�P���i�y�j�P�Q���i���j�ɓ����őS���ψ���E�S��������c��������܂��A��肩�珬�{�R�A�����A�؉��A�{�{�A�ɓ��̂T�l�̐搶���Q�����邱�ƂɂȂ��Ă��܂��B
�� �g�ƒ�̎Z���E���w�S�ȁh�i���{�]�_�Ёj�̔���s���́A�ƂĂ��킩��₷���u�Q����тȂ���ł��ǂ߂鎫�T�v�Ƃ������ƂłƂĂ��D���̂悤�ł��B�T�[�N���̂U�������҂ɓ����Ă��܂��̂ŁA���̂߂g���|���h�Ŏ�ɓ���͂��ł��B�l�ł܂��w�Z�̐}���قɕ��y���������̂ł��ˁB
�� ��D���̋{�{�搶�Ɖ����搶�̃z�[���y�[�W�B�{�{�搶�̃z�[���y�[�W�̒��ɓm�˃T�[�N���̃R�[�i�[������܂��B�F����̂����Ă݂悤�B�����搶�̂g�o�̒��ɑS�����̃R�[�i�[������܂��B�Ƃ��ǂ��A�N�Z�X���Ă݂Ă��������B
�@�@�@�����搶��HP�@�@http://www5b.biglobe.ne.jp/~simomac/
�@�@�@�@�{�{�搶��HP�@�@http://homepage1.nifty.com./toretate/
�P�Q�����̗l�q
�� �a�`�c�ɁA���p�̂Q�������Ɛ����̔�̒藝��K�p����
�b�`�F�b�c���`�h�F�h�c�E�E�E�E�@
���l�Ɂ��a�`�c�ɓK�p���āA
�a�`�F�a�c���`�h�F�h�c�E�E�E�E�A
���s�v�c�ȍs��@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ɓ�����i�����k���Z�j
�@���ϕ��̑n�����A�j���[�g���͓����̌v�Z�����̂悤�ɂ��Ă����炵���B
![]()
����![]() �����ɏ������ʂȂ�A
�����ɏ������ʂȂ�A![]() �͖����ł���قǏ������ʂł���̂ŁA
�͖����ł���قǏ������ʂł���̂ŁA
![]()
�Ƃ݂Ȃ��āA
![]()
�Ƃ���B������![]() �̑����̊�����
�̑����̊�����![]() �ł���̂ŁA
�ł���̂ŁA
![]()
�ƂȂ�B���̂悤�ɂ��Ċ�![]() �̓W�J���ɂ�����
�̓W�J���ɂ�����![]() �Ƃ���
�Ƃ���
![]()
�œ��������߂Ă����Ƃ����B
�@�������`���_���ɂ���
�u![]() �Ȃ̂�
�Ȃ̂�![]() �v�E�E�E�@
�v�E�E�E�@
�Ƃ͂������Ȃ��̂��H�܂��A
�u![]() ��������
��������![]() �v�E�E�E�A
�v�E�E�E�A
�ł͂Ȃ����H�ȂǂƂ����ᔻ�����������B�����͖������̃L�`���Ƃ����莮�����Ȃ���Ă��Ȃ����炱�̂悤�ȍ��������c�_�́A����Ӗ��œ��R�̂��Ƃ������B
�@���̂悤�ȍs��̏W�����l���悤�B
![]() ������
������![]() �͎���
�͎���
�����ŁA
![]()
�Ƃ���ƁA
![]()
�ƕ\�����B
![]()
�i![]() �͗�s��j
�͗�s��j
�ł��邩�炱�̃^�C�v�̍s��̂����Z�A�Ђ��Z�A�����Z�͎��̂悤�ɂȂ�B
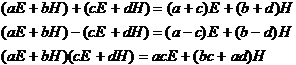
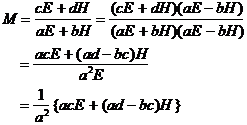
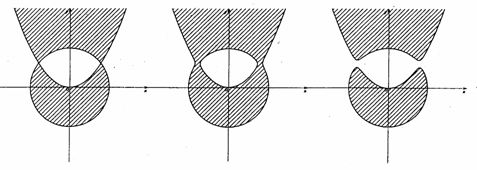

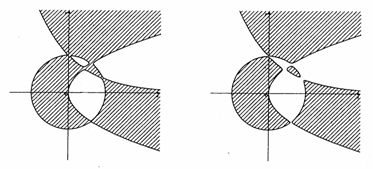



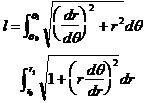
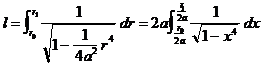
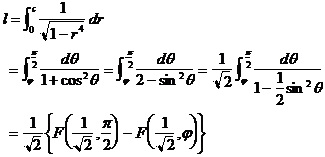

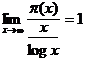 �ɂ��Ăǂ��v���B
�ɂ��Ăǂ��v���B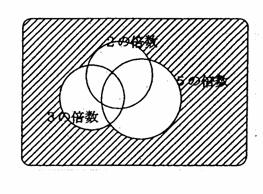
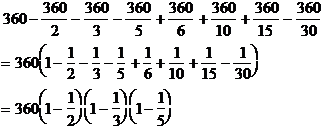
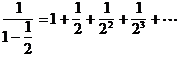
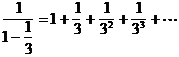 �A
�A