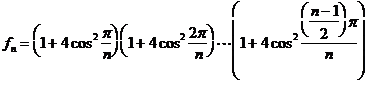�@�f06�m�˃T�[�N���R�����̈ē�
�@�����������������z���܂������A�m�˃T�[�N���̉���̊F�l�N�x���̌�������ꂳ�܂ł��B���āA�m�˃T�[�N���̂R���������̓����ł����܂��B����̃T�[�N���́A�����P�F�O�O����s����S�����̏�����̂��ƈ�������������܂��B�܂��A����������̉��X���i�_�ސ��j���Q������\��ł��B�Z�������ł����A�V�������Ԃ�U���ĎQ������悤��낵�����肢���܂��B�܂��A�T�[�N���I���ア���̌������Łg���̐ߋ���j����h�����\��ł��̂ŁA��낵�����肢���܂��B
�L
�P�@���@ ���@�R���S���i�y�j�����S�F�O�O�`�V�F�O�O
�Q�@��@ ���@����w����w���@���{�R�������S�O�V���j
�@�@�@�@�@ �@ �@tel
019-621-6539 fax 019-621-6543
�R�@���@�@�@ �@�e ���H���|�[�g���\�E�����A
�@�@�@�@�@�@�@�@ �@�@������&
���w����
�C���t�H���[�V����
�� �R���S���i�y�j�P�F�O�O〜�R�F�T�O����w����w���ł`�l�h�S�����̑�S����s�ψ��������܂��B�T�[�N������̊F�l�͂ł��邾���s�������Ă�����̕����Q�����Ă��������B���̎��s�ψ���ɂ͒������牽�X�搶�A���k�n�拦�̊e���̎��s�ψ����Q�����邱�ƂɂȂ��Ă��܂��B
�� �Q���P�P���i�y�j�ɓ����őS���ψ���Ɋ�肩�珬�{�R�A�����A�؉��A�{�{�A�ɓ��̂T�l�̐搶���Q�����A���N�̑S�����̓��k�n�拦�̒�Ă��ꕔ�C������ĔF�߂��܂����B���悢�揀�����n�܂�܂��܂��B
�� �Q���P�Q���i���j�ɓ����őS��������c��������܂����B�o�h�r�`�Q�O�O�R�i�n�d�b�c�̊w�K���B�x�����j�̓��{�̐��w����ɗ^�����V���b�N�ɂ��Ă̕Ɠ��_�ł����B���ѓ������i������j�ɂ��g�I���h������ƂĂ��ʔ��������ł��B����ɂ��Ă����ȏȂ̊y�ϓI�Ƃ���������߂ɂ͋^��������܂����B���ϓ_���Q�������U�ʂŃg�b�v�O���[�v�Ƃ������߂͂܂��悢�Ƃ��āB���w�ւ̋����S�Ɋւ���S�̎��⍀�ڂ́A�Q�����̒��ŕ�����Ȃ��Œ�O���[�v�ł���ɂ��ւ�炸�A�������P�s�g���ς�菭�Ȃ������h�ōς܂��Ă��܂��B���̎��⍀�ڂ́g�����̐��w�w�͂̃|�e���V�����G�l���M�[�̕\���h�Ȃ̂ł��̂悤�ȕ��ȏȂ́g���������̂ɂӂ��h�̗���́A���w����̖����Ɂg�É_�h�������炷�C�����܂��B
�� �S���P���A�Q���ɋ��s�̐���@�ł`�l�h�̑S�����Z�W��\�肳��Ă��܂��B���N�̉Ԋ����̐�`�����˂Ă����܂��H
�� �g�ƒ�̎Z���E���w�S�ȁh�i���{�]�_�Ёj�̔���s���́A�ƂĂ��킩��₷���u�Q����тȂ���ł��ǂ߂鎫�T�v�Ƃ������ƂłƂĂ��D���̂悤�ł��B�T�[�N���̂U�������҂ɓ����Ă��܂��̂ŁA���̂߂g���|���h�Ŏ�ɓ���͂��ł��B�l�ł܂��w�Z�̐}���قɕ��y���������̂ł��ˁB
�� ��D���̋{�{�搶�Ɖ����搶�̃z�[���y�[�W�B�{�{�搶�̃z�[���y�[�W�̒��ɓm�˃T�[�N���̃R�[�i�[������܂��B�F����̂����Ă݂悤�B�����搶�̂g�o�̒��ɑS�����̃R�[�i�[������܂��B�Ƃ��ǂ��A�N�Z�X���Ă݂Ă��������B
�@�@�@�����搶��HP�@�@http://www5b.biglobe.ne.jp/~simomac/
�@�@�@�@�{�{�搶��HP�@�@http://homepage1.nifty.com./toretate/
�Q�����̗l�q
�@��N���Ɏ��ƂŐ���̑Q������������B���x����Ă��Q�����͓���B����͖{���Q�[���I�ȓ��e���܂�ł���̂ŁA�y���߂鋳�ނȂ͂������A���ꂪ���L���ŗh�炢�ŁA�Q�����Ńg�h���������A�Ō�͐��w�I�A�[�@�ʼn_�U��������Ƃ����p�^�[�ɂȂ肪���ł���B�I����Ă݂�g����Ȃ匙���I�h�Ƃ������ƂɂȂ�B
�@�f�p�Ȑ���́A���Ƃ��Ɛl�̍D��S��T���S���������D�̋��ނȂ̂�����A���̑f�ނ̂悳�������g�����@�h���J������K�v������̂ł͂Ȃ����낤���B
�@�Q����![]() �ɂ��čl���悤�B����
�ɂ��čl���悤�B����![]() �Ƒ�Q��
�Ƒ�Q��![]() �����낢��Ȓl�ɂ��Ă��̕ω��ׂĂ݂悤�B
�����낢��Ȓl�ɂ��Ă��̕ω��ׂĂ݂悤�B
![]() �̂Ƃ��@�@
�̂Ƃ��@�@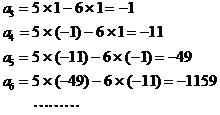 �@�@
�@�@![]() �̂Ƃ��@�@
�̂Ƃ��@�@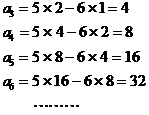
![]() �̂Ƃ��@�@
�̂Ƃ��@�@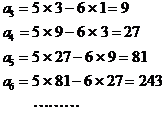 �@�@�@�@�@�@
�@�@�@�@�@�@![]() �̂Ƃ��@�@
�̂Ƃ��@�@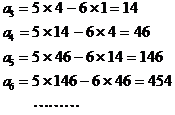
![]()
�����Ȃ̂ŁA
![]()
�����藧�͂��ł���B����
![]()
���A���̕������i���ꂪ�������������I�j�̉��ɂȂ�B�܂�
![]() �@���@
�@���@![]()
![]()
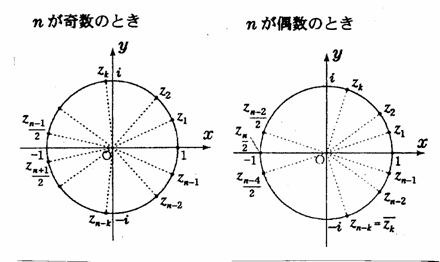
�̂Ƃ��́A�ǂ̂悤�ɂ�����悢���낤���B���܂���Ɍ���Q�ƌ���R�̓��䐔��ɕ�������悢�̂ŁA���̘A�����������Ƃ��B
![]()
��������ƁA
![]()
�����܂�B�����ŁA
![]()
�Ƃ��Ē�������@�����s���Ă݂悤�B
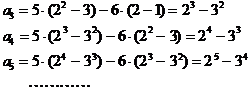
������A
![]()
�������̂��琳���ʑ̂��o���@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�{�@���Y�i���Γ썂�Z�j
�@�����Ȃ́u�ۑ茤���v�Ŕ��A�X�`���[���̗����̂��琳���ʑ̂��o���e�[�}�Ɏ��g���Z���̌����������Љ�܂��B
�@�͂��߂�
�@������A�ۑ茤���̑�ނɂ��Ď��B���Y��ł���ƁA���ς��߂�H�ׂĂ����搶�������܂����B���������������ɐH�����Ƃ��搶���A�����͂��ς��߂��������茩�߂Ă��܂��B���������������ȂƎv���B�߂Â��Ă݂Ă݂�ƁA�l�Q�Ɍ`�������������p�`�����Ă��܂����B�����Ƃ���ɂ��ƁA����͋{�{�搶�̂��萻�̂��ς��߂��Ƃ������Ƃł��B
�@��搶�ƈꏏ�ɂ��ς��߂����\������A�����{�{�搶�̂Ƃ���ɍs���܂����B�u���̑卪�A�ǂ�����Đ�����ł����I�H�v�u����͂ȁA�����������Ă���ʂ����s�ŁA�����̒��_�����̕ӂɂȂ���悤�ɐ��Ă����ƁE�E�E�v
�@�Ȃ������������������̂ł����A���퐶���ł͂������A���w�̎��Ƃł��߂����ɐG��邱�Ƃ̂Ȃ����܊p�`���P�Q���������Ă��闧�̂̐������A�卪�ł��ꂽ���ĕ�����Ȃ��̂ł��B���ς��߂����ł͑���Ȃ���搶���悻�ɁA���B�̌������n�܂�܂����B
�@�Q�O�O�T�N�V���Q�T���@
�@�@���\��ʑ̂ɓ��ڂ��閼�h���H��
�@�Q�O�O�T�N�V���Q�U���@
�@�@�P�ӂ̒����P�̗����̂��琳�l�ʑ̂����o�����߂̌v�Z
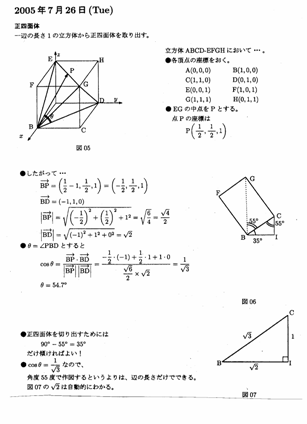 �@�Q�O�O�T�N�V���Q�V��
�@�Q�O�O�T�N�V���Q�V��
�@�@�Œ��for���l�ʑ̂���낤�E�E�E�v�Z�E�E�E
�@�Q�O�O�T�N�V���Q�W���@
�@�@�Œ��for���l�ʑ̂���낤�E�E�E���P�E�E�E
�@�Q�O�O�T�N�V���Q�X���@
�@�@�Œ��for���l�ʑ̂���낤�E�E�E���Q�E�E�E
�@�Q�O�O�T�N�W���@�Q���@
�@�@������ƌ����Ă����I�I
�@�Q�O�O�T�N�W���@�W��
�@�@Zome Tool�Ő��\��ʑ̂�g�ݗ��ĂĊώ@
�@�Q�O�O�T�N�W���@�X���@
�@�@���\��ʑ̂����W�ōl����
�@�Q�O�O�T�N�X���P�U���@
�@�@�Ђ�����v�Z
�@�Q�O�O�T�N�X���P�W���@
�@�@����\�ʑ̂̊e�ʂ̐��O�p�`�̒��S������ł����Ɛ��\��ʑ̂��ł���B
�@�Q�O�O�T�N�X���Q�P���@
�@�@���\��ʑ̂��݂�
�@�Q�O�O�T�N�X���Q�Q���@
�@�@���\��ʑ̂�����
�@�Q�O�O�T�N�P�O���R���@
�@�@����\�ʑ̂ɂ���
�@�Q�O�O�T�N�P�O���P�S���@
�@�@����\�ʑ́@���Ă݂܂����E�E�E�B�Ȃ������т��������
�@�Q�O�O�T�N�P�O���Q�W���@
�@�@����\�ʑ̂����̂ɁA�܂��\��ʑ̂�����Ă������B
�@�Q�O�O�T�N�P�P���Q�Q���@
�@�@����\�ʑ̂̓�〜�i���̒�Ȃ���〜
�@�Q�O�O�T�N�P�P���Q�T���@
�@�@�Ђ�����v�Z
�@�Q�O�O�T�N�P�P���Q�X���@
�@�@����\�ʑ̂Â��@������͏C�w���s
�@�Q�O�O�T�N�P�Q���P�U���@
�@�@�܂Ƃ߂ɐ���
�@�Q�O�O�T�N�@
�@�@�P���P�R���@���܊p�`�ɂȂ�̂��H
���̌����́A���̉ۑ茤�����\��łȂ�ƂP�ʂɋP�����Ƃ̂��Ƃł��B
�����[�}���̃[�[�^���ɂ���〜�C�m�_���T�v〜�@�@�@�@�@�@���X�؋`��i����@���j
�@�C�m�_���̓��e�̓��[�}���[�[�^���̕��ϒl���_�Ɋւ��邢�낢��Ȍ��ʂ������T�[�x�C�_���ł���B
�@���[�}���[�[�^���Ƃ͎��̂悤�Ȋ��ł���B
![]() �@�������A
�@�������A![]()
![]() �ɂP�ʂ̋ɂ����L���^���Ƃ��đS���f���ʂɉ�͐ڑ������B
�ɂP�ʂ̋ɂ����L���^���Ƃ��đS���f���ʂɉ�͐ڑ������B
�������@![]()
���[�}���[�[�^���͑f���̕��z�ȂǁA�����_�Ɩ��ڂɊW���Ă���A���ꎩ�g���ɋ������錤���Ώۂł���B�܂��A���[�}���\�z�A�����f���[�t�\�z�Ȃǂ܂��܂��������̖�������B
�@���[�}���\�z�́A�[�[�^����![]() �ɂ������_�͂��ׂ�
�ɂ������_�͂��ׂ�![]() ��ɂ���Ƃ����\�z�ł���B
��ɂ���Ƃ����\�z�ł���B
�@�C�m�_���Ɋ֘A����L�[���[�h�͑�܂��ɂR�グ����B
�@�@�@�@�P�D���[�}���\�z
�@�@�@�@�Q�D�����f���[�t�\�z
�@�@�@�@�R�D���ϒl���_
�@
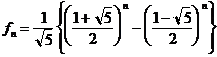 �E�E�E�i�P�j
�E�E�E�i�P�j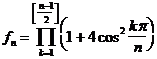 �E�E�E�i�Q�j
�E�E�E�i�Q�j